在我上大學的時候，不少關於 X 的課程始於下面這樣的問題：

1. 什麼是 X？（X 的定義）
2. 學好 X 在理論上有什麼意義？
3. 學好 X 在實踐上有什麼意義？
4. 怎樣學好 X？……

然後給出一些答案和細節，構成該課程的「緒言」。近年來，一些新出版的敎科書仍沿襲這樣的慣例，甚至「讀經風」也要從「爲什麼要讀」「讀什麼」和「怎樣讀」等問題颳起。這門課叫「符號邏輯」，是當代邏輯即數理邏輯的入門課程。按慣例，好像也該先講講什麼是邏輯，什麼是符號邏輯，什麼是當代邏輯，爲什麼要學及如何學好邏輯，等等。

像「邏輯是什麼」或「當代邏輯是什麼」這類問題，如果問的是邏輯或當代邏輯等的定義，那麼我勸初學者不必太認眞。初學邏輯，自然想知道邏輯學大概是怎麼回事，想知道邏輯學家大概做些什麼。但是，若想滿足這種好奇心，與其在腦子裏裝些不明不白的「定義」，倒不如對邏輯學裏討論的問題以及討論的方法多一點認眞。這是因爲：對一個學科的整體上的理解，是以對該學科中的問題和方法的理解爲前提的。當然，這並不是說，關於邏輯或數理邏輯的各種說法都不值得思考。這裏的要點是：不具備足夠邏輯知識的人，分不出這些說法的好壞高低，反而容易因爲學了某些「定義」「分類」或「方向」，就自以爲有些「邏輯學問」甚至「超邏輯學問」了。待到眞有點邏輯學問後，再來思考這類問題爲時不晚——只要那時還有這種興趣。

在這門課上，把邏輯作爲學科來談時，通常都是指當代的形式邏輯，也稱當代邏輯、現代邏輯或（廣義）數理邏輯。我們雖不定義邏輯是什麼，但以普通人的知識爲背景，我們可以隨便談談邏輯學大概討論些什麼問題。關於邏輯學有以下幾種說法：

1. 邏輯學是關於論說（argument）的。
2. 邏輯學是關於推理（inference, reasoning）的。
3. 邏輯學是關於理論或信念的一致性（consistency）的。

論說

無論是關於整個世界的某種看法，還是關於一類事物的某種理論，都是由一些句子來表達的。這些句子大體上可以分爲兩類：眞句子和假句子。

在很多情況下，確定一個句子的眞假的最基本方法是直接考察句中所談的事物。但是，直接考察經常是做不到或不易做到的。因而，爲確定一給定句子 $\varphi$ 的眞假，人們往往需要比較 $\varphi$ 和某些已知其眞假的句子 $\psi_0$,…,$\psi_n$。即使只考慮是否應該相信 $\varphi$，我們也常需比較 $\varphi$ 和某些我們相信或不相信的句子 $\chi_0$,…,$\chi_n$。從 $\psi_0$,…,$\psi_n$（或 $\chi_0$,…,$\chi_n$）到 $\varphi$ 或其否定的過渡，通常被稱爲「推理」。［Henkin,1967］

在上述語境中，$\psi_0, \cdots, \psi_n$（或 $\chi_0, \cdots,\chi_n$）常被稱爲「前提」，$\varphi$（或其否定）常被稱爲「結論」。人們把一集前提和從它得出的結論合起來，稱之爲論說，亦稱論證（argument）。這裏，「推理」指從前提得出結論的過程，而「論說」指前提和結論的集合。

考慮下面的兩句話，從中我們能得出什麼結論？

示例 0.0

1. 人人都愛我的寶寶。
2. 我的寶寶只愛我。

人們可以去編些故事，比如説，「我」指某人，「寶寶」指她（他）的孩子或情人，等等。但假定張三説，他從示例 0.0 得出「我的寶寶就是我」，我們會同意嗎？張三是這樣得出他的結論的（用「寶寶」代替「我的寶寶」）：

既然人人愛寶寶，而寶寶是人，所以寶寶愛寶寶。「寶寶只愛我」說的是：對任何 $x$，如果寶寶愛 $x$，那麼 $x$ 就是我；從而如果寶寶愛寶寶，那麼寶寶就是我。既然寶寶愛寶寶，所以寶寶就是我。

通常人們用下述方法表示一個論說：將其前提和結論列出，用一道線將前提與結論分開，並在結論前加上「$\therefore$」表示「所以」。比如，張三從示例 0.0 中的前提到結論「我的寶寶就是我」的論說就可以表示爲

示例 0.1

1. 人人都愛我的寶寶。
2. 我的寶寶只愛我。
3. 所以，我的寶寶就是我。

論說的好壞

論說有好有壞。邏輯學要做的事情之一，就是區分好的論說與壞的論說，或者說是給出一般的方法，而依據這些方法，我們能對論說的好壞作出正確的判斷。這大概是對邏輯的最常見的一種說明。要說明上述示例是否好的論說，先要說明什麼樣的論說是好的，什麼樣的是不好的。對此，最直觀又最簡單的說法與下面說的差不多：

對任何一個論說，如果在每個使其前提都眞的情況下，其結論也一定眞，那麼這個論說是好的；如果在某些情況下，該論說的前提都眞而結論假，那麼這個論說就是壞的（不好的）。

這種直觀的說法可以讓人對論說的好壞有個初步的印象，但不夠清楚準確。比如，什麼叫作「使前提都眞的情況」，什麼叫作「在某個情況下，一個命題是眞的」，等等，現在都還不清楚。這種說法的優點，是它強調了論說的好壞不在於前提和結論的眞假，而在於它們的眞假在不同情況下的比較。

論說形式的好壞

一個具體論說的好壞與其前提和結論的眞假無關：一個好論說的前提和結論可能都是假的，而一個壞論說的前提和結論也可能都是眞的。（注：論說本身的好壞與論說形式的好壞是相互區別而又有聯繫的兩個問題。）比如下面這個論說：

示例 0.2

1. 企鵝都是鳥。
2. 猴子都不是企鵝。
3. 所以，猴子都不是鳥。

它的前提和結論都是眞的，但人們僅憑直觀就知道這個論說是不好的；人們會說：不是企鵝的不一定就不是鳥，比如說麻雀就不是企鵝，但不能因此說麻雀不是鳥。企鵝的確都是鳥，猴子的確都不是企鵝，並且猴子也的確都不是鳥；但是，最後一個命題之前的「所以」是沒道理的。再看下面的論說：

示例 0.3

1. 愛運動的學生學習成績都很好。
2. 男學生都愛運動。
3. 所以，男學生學習成績都很好。

它的前提和結論都是假的，但整個論說似乎無懈可擊。

常聽到爭論中的人說：「即使你的論證沒問題，你的前提本身就是假的，結論當然也是假的。」這是一種常見的誤解，彷彿好論說會「保存」虛假性，即會把前提的虛假性傳到結論上。下例表明好論說並不保存虛假性：

示例 0.4

1. 所有的貓都是人。
2. 所有的學生都是貓。
3. 所以，所有的學生都是人。

易見兩個前提都是假的，結論是眞的，而整個論說也無懈可擊。

前提有眞有假的好論說或壞論說的例子也很多，不一一列舉了。一般說來，眞、假前提和眞、假結論的各種組合情況，就壞論說而言都是可能的；就好論說而言也差不多，只有一個例外：好論說不會有眞前提和假結論。

上面説過，對任何一個論説，如果在每個使其前提都真的情況下，其結論也一定真，那麼這個論説是好的。所謂使前提都真的情況，簡單地説就是能使所有前提同時成立的一種解釋，而這種解釋既可以是現實也可以和現實無關。比如我們討論示例 0.2 中的壞論説時，給出的理由是「麻雀不是企鵝，但不能因此而説麻雀不是鳥」。這相當於把「猴子」換成了「麻雀」或是把「猴子」解釋成了麻雀。當然，這是不夠清楚的説法。清楚一些的説法涉及「論説的形式」（argument form）。

我們暫時依賴直觀判斷什麼是一個論說的形式。比如下面是個具體的論說，以及它的形式：

示例 0.5

1. 所有的貓都是人。
2. 張三是貓。
3. 所以，張三是人。

1. 所有 $S$ 是 $P$。
2. $a$ 是 $S$。
3. 所以，$a$ 是 $P$。

再如下列是示例 0.2 、示例 0.3 的論證形式：

示例 0.6

1. 所有 $S$ 是 $P$。
2. 所有 $Q$ 都不是 $S$。
3. 所以，所有 $Q$ 都不是 $P$。

1. 所有 $S$ 是 $P$。
2. 所有 $Q$ 是 $S$。
3. 所以，所有 $Q$ 是 $P$。

不同的論説可以有相同的形式，而具有相同形式的論説稱爲這個論説形式的特例（instance）。例如，示例 0.7 中有兩個不同的論説，但它們的形式同是示例 0.6 上列之形式，並且同是該形式之特例。

示例 0.7

1. 企鵝都是鳥。
2. 猴子都不是企鵝。
3. 所以，猴子都不是鳥。

1. 企鵝都是鳥。
2. 麻雀都不是企鵝。
3. 所以，麻雀都不是鳥。

一個論說形式的眾多特例中有一類被稱爲「反例」。一個論說形式的反例（counter exampIe）是這個論說形式的特例，其所有前提都是眞的，而其結論是假的。如果一個論說形式沒有反例，那麼該論說形式是好的；如果一個論說形式有反例，那麼該論說形式是壞的（不好的）。

論說好壞取決於形式的好壞

一個論說的形式是好的（亦即它的形式沒有反例），則稱其爲好的論說。一個論說的形式是壞的（亦即它的形式有反例），則稱其爲壞的論說。

既然具體論說的好壞在於它的形式的好壞，那麼就任何具體論說而言，它的（前提和）結論眞不足以說明它好，而它的（前提和）結論假也不足以說明它壞——它的好壞在於同樣形式的特例中有沒有前提眞而結論假的論說。由此可知，要說明一個論說是壞的論說，最直接的方法是去找一個與它形式相同且前提眞而結論假的論說。

我們來看如何説明一個論説是壞的論説。先考慮示例 0.7 右側的論説，易見它的前提都真而結論假；我們知道其形式是示例 0.6 左列之形式，所以它是示例 0.6 左列形式的反例。既然示例 0.6 左列形式有反例，它就是壞的論説形式。現在來看示例 0.2 中的論説，亦卽示例 0.7 左側的論説，其形式也是示例 0.6 左列之形式。我們現在知道示例 0.6 左列形式是壞的論説形式，所以，示例 0.2 中的論説是個壞的論説。我們來看另一個論説：

示例 0.8

1. 浩畢特都生活在沙伊鄂。
2. 拜根斯都是浩畢特。
3. 所以，拜根斯都生活在沙伊鄂。

1. 所有 $S$ 是 $P$。
2. 所有 $Q$ 是 $S$。
3. 所以，所有 $Q$ 是 $P$。

在了解「浩畢特」「沙伊鄂」和「拜根斯」的意思之前，我們無法判斷示例 0.8 左列論證的前提或結論的真假。但是，我們知道其的形式是示例 0.8 右列之形式。

這個形式有下述特點：無論把什麼類名詞放在 S，P 或 Q 的位置上，都不會得到具有真前提和假結論的論説，卽不會得到示例 0.8 右列形式的反例。這就是説，示例 0.8 右列之形式是好的論説形式。因爲示例 0.8 左列之形式是示例 0.8 右列之形式的特例，所以它是個好的論説。

然，説一個論説形式沒有反例，並非僅僅是説沒有找到它的反例，因爲沒找到反例不等於沒有反例。示例 0.8 右列之論説形式比較簡單，容易看出它不會有反例；但是，一個好的論説形式可以很複雜，僅靠直觀未必能説出它是否有反例。這門課程的任務之一，就是學會判別好壞論説形式的若干方法。

如果承認一個論說是好的，那麼接受其前提就無法理性地拒絕其結論，從而否定其結論也就無法理性地堅持其前提；如果斷定一個論說是壞的，那麼接受其前提的同時可以拒絕其結論。用邏輯術語來說，如果一個論說是好的，那就意味着它的前提「邏輯蘊涵」（logically implies）它的結論（當代邏輯不僅討論給定命題集合是否邏輯蘊涵某給定命題，它更要突破具體命題和具體命題集合的限制，把邏輯蘊涵關係作爲對象來討論。），或者說結論是前提的「邏輯後承」（logical consequence）；如果一個論說是壞的，那就意味着它的前提和結論之間沒有邏輯蘊涵關係，亦即結論不是前提的邏輯後承。我們將在第一編中討論邏輯蘊涵的一種簡單形式——重言蘊涵（重言後承），而在第三編中討論邏輯蘊涵（邏輯後承）。

演繹

前面列舉的關於邏輯學的幾種說法中，有一種是「邏輯學是關於推理的」。當談到論說的好壞與推理的關係時，也有類似於下述命題的說法：對任何一個論說，如果從其前提能夠合理地推出其結論，該論說就是好的；如果從其前提不能合理地推出其結論，該論說就是壞的（不好的）。

所謂「合理地推出結論」，通常被理解爲一個末端是這個結論的推理鏈（chain of reasoning），它可以只有一兩步，也可以有很多步，但（關鍵的是）每一步都要「合理」。對「合理性」的各種要求或解釋，形成了不同類型的推理鏈。演繹（deduction）是這些類型中的一種。

演繹對「合理性」的基本要求是：「推理鏈」中的每個推理步驟，如果不是前提、定義、預設、公理、假設等或已經從這些東西「合理地」推出的命題，那麼一定是從它們用某些明確的規則得到的。這些明確的規則都要有如下性質：在演繹中使用這些規則時，人們從眞命題只能得到眞命題。眾所周知的各種三段論、假言推理規則和選言推理規則等就屬於這種規則。（演繹中也常用被稱之爲「引理」和「定理」之類的東西。它們雖與公認的規則不同，但因爲它們也是經演繹得到的，所以可以把它們看作是已經「合理地推出」的命題。）如此說來，至少直觀上看，演繹像是將一個個好的論說接起來——它一步步推出的每個命題都是該命題前面某些命題的邏輯後承。

演繹的例子一

數學證明都是演繹的例子，我們就不列舉了。這裏來看另一類例子。上一節談到示例 0.1 之論說，我們曾假定張三給岀了他的說明。那個說明其實就是個演繹的例子。雖然那個說明中的命題並沒有列成鏈，而對每一步到下一步的過渡，也沒說明是運用了什麼規則；但是，人們可以把那個說明「還原」成符合上述說法的演繹：

示例 0.9

1. 所有的人都愛我的寶寶。➠ 前提（經過複述）
2. 我的寶寶是人。➠ 預設
3. 我的寶寶愛我的寶寶。➠ 三段論
4. 我的寶寶只愛我。➠ 前提
5. 對每個 $x$，如果我的寶寶愛 $x$，那麼 $x$ 就是我。➠ 「按定義改寫」
6. 如果我的寶寶愛我的寶寶，那麼我的寶寶就是我。➠ 特例
7. 我的寶寶就是我。➠ 肯定前件的假言推理（modus ponens）

上述演繹「還原」的文字過程，可按照後續章節介紹的謂詞邏輯的自然演繹方法表現。設定論域爲人，$\mathbf{a}$ 爲「我」，$\mathbf{b}$ 爲「我的寶寶」，$Px$ 表示「$x$ 是人」，$Lxy$ 表示「$x$ 愛 $y$」，則本例推理過程可表述爲（學完相關章節後再閱讀這個自然演繹的例子）：

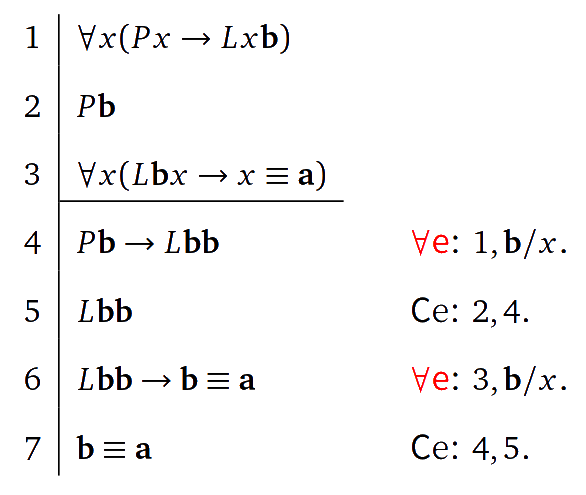
當然，這個例子難免讓人覺得怪。比較近情理的一個說法是：對於「所有的人都愛我的寶寶」這句話，人們往往不把其中的「所有的人」理解爲所有的人，而是理解爲寶寶以外的所有人。根據這種說法，從「所有的人都愛我的寶寶」應該得不出「我的寶寶愛我的寶寶」，進而從上述兩個前提應該得不出「我的寶寶就是我」這個結論。

「所有的人」的這種「…以外的所有的人」的用法，是個習慣或語境的問題，而非命題的邏輯結構或推理的問題。顯然，我們不能說「所有的人」的意思就是「寶寶以外的所有的人」的意思，因爲在「所有的人都要睡覺」「所有的人都要喫飯」等句子中，「所有的人」顯然不是指寶寶以外的所有的人。當然我們就更不能說「所有的 $S$ 是 $P$」中的「所有的 $S$」應理解爲寶寶以外的所有的 $S$。如果把「所有的人都愛我的寶寶」的形式概括爲「所有的 $S$ 都與 $a$ 有關係 $R$」（其中 $a$ 是某個 $S$，就像我的寶寶是人），那麼「所有的 $S$」在句子中的意思是否就是所有不等於 $a$ 的 $S$ 呢？有些時候是這樣，但顯然也並不總是這樣。

比如，正常人不會認「所有的正整數都大於 1」這一命題是眞的，因爲正整數 1 不大於 1。然而，假如「所有的正整數」的意思就是所有不等於 1 的正整數，那麼我們就必須承認這是個眞命題。這樣的例子太多了。日常會話中，我們習慣於怎麼省事怎麼說，「差不多就行」，甚至應該儘可能避免繁瑣。但我們談到理論問題時，「差一點」也不行。上面的例子告訴我們，如果在我們的理論中，我們把下列命題中的「除了 $a$」漏掉了，

1. 所有的 $S$ 都與 $a$ 有關係 $R$，除了 $a$.
2. $a$ 是 $S$ 且只與 $b$ 有關係 $R$.

那麼「$a$ 就是 $b$」就成了從我們理論中可以演繹出來的一個結論，儘管我們可能並不想要它。

演繹的例子二

我們來看另一個演繹的例子。據說，有人曾針對古典邏輯（注：「古典邏輯」是狹義的數理邏輯的另一個名字。狹義的數理邏輯包括「四論」（公理集合論、模型論、遞歸論和證明論），也包括本書討論的命題邏輯和一階邏輯等理論。在當代邏輯範圍內，古典邏輯範圍外，還有眾多邏輯分支，俗稱「非古典邏輯」。）「從假命題可推出任何命題」這一特點向羅素挑戰，要他從「2+2=5」推出「羅素和敎皇是同一個人」，羅素當即以下述演繹（或類似的演繹）作出回應：

示例 0.10

1. 2+2=5 ➠ 假設
2. 2=3 ➠ 等詞法則（等式兩邊各減 2）
3. 3=2 ➠ 等詞法則（對稱性）
4. 2=1 ➠ 等詞法則（等式兩邊各減 1）
5. 羅素和敎皇是兩個人。 ➠ 事實
6. 羅素和敎皇是同一個人。 ➠ 等詞法則（運用上述「2=1」）

這個演繹也有點「怪」。上一個例子的前提「所有的人都愛我的寶寶」，雖然未必是眞的，但在某些情況下可能是眞的，至少我們不知道它是否在任何情況下都是假的。在這個例子中，我們卻知道前提「2+2=5」在任何情況下都是假的。演繹和好的論說一樣，它並不考慮前提或結論的眞假。只要推演規則的選擇適當，運用這些規則得到的命題都是前提的邏輯後承，亦即演繹保存眞實性。正因如此，演繹不僅僅可以用來（從正面）說明某個命題的眞實性，它同樣可以用來（從反面）說明某個命題的荒謬性。當然，演繹並不保存荒謬性，可以從荒謬的命題演繹出的不僅僅是荒謬的命題。

可演繹性、可證性和獨立性

如果從一集命題（理論、前提或假設）演繹出了某個命題 $\varphi$，那麼 $\varphi$ 當然是從這集命題可演繹（deducible）的。從集命題可演繹的常被稱爲這集命題的演繹後承（deductive consequence）。沒有前提的演繹稱爲證明，無需前提就可演繹的稱爲可證明的或可證的（provable）。說一個命題是不可證或從給定命題集不可演繹，不是說沒有找到它的證明或演繹，而是說不存在這樣的證明或演繹。（注：當代邏輯不僅研究某些給定命題是否可證或可演繹，它更系統地研究可證性（可演繹性）和不可證性（不可演繹性）。注意：可證性和可演繹性都是相對於演繹「系統」來談的。對於不同的演繹「系統」，一個命題是否可證或從一集命題是否可演繹的問題，完全可以有不同的答案。）

獨立性就是不可演繹性，只不過它多用於人們感興趣的命題。一個系統不可證明的命題通常很多，人們不會對所有這些命題都有同樣的興趣。人們有興趣的命題在一系統中是否不可證，常被稱爲這些命題的（相對於該系統的）獨立性（independence）問題。比如，「獨立性」很多時候被用在系統的公理上。給定一個系統和系統中的一個公理 $\varphi$。如果從 $\varphi$ 以外的所有公理經系統的全部推理規則不可證明 $\varphi$，那麼 $\varphi$ 就是獨立的。換句話說，該系統的全部推理規則和 $\varphi$ 以外的所有公理構成該系統的一個子系統，而如果 $\varphi$ 在這個子系統中不可證，我們就稱 $\varphi$ 是獨立的（independent）。對於一個系統的公理集合，如果其中每個公理都是獨立的，我們就稱這個公理集合是獨立的。

可演繹性與論說

至此，我們已經初步了解了檢驗論說好壞的兩種基本方法：演繹和對論說形式的檢驗。這兩種方法之間有沒有關係呢？

我們說過，演繹對推演規則的要求是從眞命題只能得到眞命題。讀者可能已經由此猜測：如果從一個論說的前提能夠演繹出它的結論，這個論說的形式就是好的。事實上，這個猜測是正確的，而肯定其正確性的定理稱爲「可靠性定理」。

進一步的問題是，如果從前提演繹不出結論，那是否意味着這個論說的形式一定是不好的呢？或者換個方式來問，如果一個論說的形式是好的，是否一定有一個從它的前提到它的結論的演繹呢？這個命題的答案就本書討論的演繹系統來說也是肯定的。給出這一問題肯定答案的定理稱爲「完全性定理」。

演繹和論說雖然關係密切，但它們在某些方面是很不同的。論說的好壞離不開眞或假的概念。然而，演繹在一定程度上可以是機械的，與眞和假的概念無關。對於確定的公理、假設和推演規則，我們可以逐個去試，看運用每一條公理、假設和規則能得到什麼；而只要有足夠長的時間和足夠大的空間，凡是可演繹出來的命題，我們終究可以找到它的一個演繹。雖然這種辦法很笨，而且誰也沒有那麼多時間把公理、假設和規則一個個地去試；但從理論上說，用這種笨辦法總能找到可演繹命題的演繹。這裏的關鍵是：在構造或尋找演繹的過程中，人們可以完全不考慮命題的眞假，甚至可以根本沒有眞和假的觀念——他們可以僅僅把規則運用於各個命題，而且在這樣運用時又僅僅考察這些命題的形式結構。

一致性

關於一致性的基本想法

通常，我們可以說某人言行（不）一致，指的是此人說的和做的（不）一樣。這和邏輯裏說的一致性不同。邏輯裏說的一致性（consistency），從直觀上說就是不自相矛盾，不自打嘴巴，或者是能說得過去，能自圓其說，或者是相關的各命題可以相安無事，等等。（注：參見 §2.5.3（P.88）中的「可滿足性」分析。）也有人把一致性叫作自恰。有時我們也會說一個理論和另一個理論不一致，或一組信念與另一組信念不一致，等等。在這種情況下，我們的意思是說，把這兩個理論或這兩組信念合在一起就不一致。

很多時候，說一個理論（或一集信念）是一致的，意思是說，在適當的解釋下，這個理論中的所有命題都同時是眞的；而說一個理論（或一集信念）是不一致的，是說在任何解釋下，這個理論中的命題都不會同時是眞的。這種一致性的觀念是一種「語義」觀念，我們可以稱它爲「語義一致性」。當代邏輯中還有另一種一致性的觀念：對於每一個理論，如果從它不能演繹出任何一對矛盾的命題，那麼它就是一致的；否則，它就是不一致的。這種一致性的觀念是一種「語法」觀念，我們可以稱它爲「語法一致性」。在當代邏輯研究中，「一致性」通常指語法一致性，而語義一致性被稱爲「可滿足性」。

語法一致性和語義一致性有如下關係：

1. 相對於給定的演繹系統，如果語義一致的理論都是語法一致的，那麼該系統一定有「可靠性」，亦即從前提可演繹的都是這些前提的邏輯後承。
2. 相對於給定的演繹系統，如果語法一致的理論都是語義一致的，那麼該系統一定有「完全性」，亦即只要是前提的邏輯後承都從這些前提可演繹。（注：這一節中有幾個命題，其眞實性對初學者來說可能不那麼明顯。我們並不打算在此處詳細討論這些命題，而會在後面討論它們。所以，即使現在不明白這些命題爲什麼成立，初學者也不必因此而對邏輯心生畏懼；讀完這本講義後回頭來看這些命題時，就會明白它們成立的理由了。）

不一致命題集的例子

一個不一致的命題集合，如果其中的命題比較簡單且數量很少，那麼它的不一致性通常容易被發現。那些直接包含矛盾的命題集顯然是不一致性的。比如：

1. 海德格爾是納粹。
2. 海德格爾不是納粹。

在任何解釋下，如果這兩個命題之一是眞的，則另一個不可能是眞的；所以任何解釋都不能使這集命題同時成立。

在一定預設或直觀背景下，有些不一致的命題集雖不是簡單地包含一個命題和它的否定，但可以導出一對直接否定對方的命題。比如：

1. 吾盾之堅，物莫能陷也。
2. 吾矛之利，於物無不陷也。

如果那個賣矛和盾的人既有矛 $a$ 又有盾 $b$，那麼由上述言論即可導致「$a$ 不能陷 $b$」和「$a$ 能陷 $b$」的矛盾。

有些命題集只含一個命題，但仍能導出矛盾的命題。比如「這位理髮師爲且只爲所有不爲自己理髮的人理髮。（注：這是集合論中羅素悖論的通俗形式，俗稱「理髮師悖論」。）」通過這個命題我們知道：

1. 這位理髮師只爲那些不爲自己理髮的人理髮（即不爲任何爲自己理髮的人理髮）。
2. 這位理髮師爲所有不爲自己理髮的人理髮。

這位理髮師要麼爲自己理髮要麼不爲自己理髮。但是，如果他爲自己理髮，那麼根據第 0 條他就不爲自己理髮；而如果他不爲自己理髮，那麼根據第 1 條他就爲自己理髮。

有些不一致的命題集合，其中任意一對命題都不導致矛盾，甚至去掉其中任何一個命題的結果都是一致的。比如：

示例 0.11

1. 哲學家都是求眞的人。
2. 求眞的人都不喜歡神侃。
3. 張三是哲學家。
4. 張三喜歡神侃。

請讀者檢查：這個命題集不一致，儘管從中任選三個命題都一致。

一致性、邏輯蘊涵與可演繹性

理論或信念的一致性和它們的「眞實性」或「正確性」是不同的。邏輯學本身不注重其他學科的具體理論或信念的眞僞，（注：從某種意義上說，邏輯學非常重視數學理論的眞僞，弗雷格和羅素等甚至深信數學可以歸結爲邏輯。這有點離題了。總之，至少可以說，邏輯學本身不注重邏輯和數學之外的具體理論或信念的眞僞。）但注重這些具體理論和信念內部各命題之間的關係，或不同理論、不同信念集合之間的關係；正如邏輯不注重具體論說的前提或結論的眞僞，但注重這些前提與結論之間的關係。一個理論或一組信念的一致性，或更一般地，一集命題的一致性，是這集命題爲眞的必要條件。如果一個理論不一致，那麼這個理論的內部有互不相容的命題，而任何一種解釋都不能使這個理論中的所有命題同時成立。一個理論或一種信念被人們相信或接受，通常不會僅僅因爲它是一致的；但如果它不一致，它就是不可接受的。

一致性與邏輯蘊涵和可演繹性是「相通」的（就本書涉及的系統而言）：

1. 如果一個理論不一致，那麼對其中的任何命題，該理論的其他命題一定邏輯蘊涵它的否定。
2. 如果一個理論是一致的，那麼對其中的任何命題，該理論的其他命題不會邏輯蘊涵它的否定。
3. 如果一個理論不一致，那麼對其中的任何命題，它的否定從該理論的其他命題一定可演繹。
4. 如果一個理論是一致的，那麼對其中的任何命題，它的否定從該理論的其他命題一定不可演繹。（注：把一致性理解爲語義一致性時，上述第三個命題等價於「完全性定理」，第四個等價於「可靠性定理」；而把一致性理解爲語法一致性時，上述第一個命題等價於「可靠性定理」，第二個等價於「完全性定理」（後兩個合起來是定理334）。）

爲了簡單地説明上述命題的意思，我們來看示例 0.11。我們説過，這個「理論」是不一致的。示例 0.11 命題 0 的否定可以從命題 1, 2, 3 演繹出來（或被它們邏輯蘊涵）：

由命題 1, 3 知，張三不是求眞的人，再與命題 2 合併，得知張三是哲學家但不是求眞的人，進而得到：有些哲學家不是求眞的人，即命題 0 的否定。

接下來我們看示例 0.11 中命題 1 的否定可以從命題 0, 2, 3 演繹出來（或被它們邏輯蘊涵）：

由命題 0, 2 知，張三是求眞的人，再與命題 3 合併，得知張三既是求眞的人又喜歡神侃，進而得到：有些求眞的人喜歡神侃，即命題 1 的否定。

至於示例 0.11 中命題 2 的否定和命題 3 的否定是否的確可以分別從其他三條命題演繹出來（或分別被它們邏輯蘊涵），這裏就不討論了，留給讀者思考。

邏輯或「邏輯」的若干問題

近年來，一些與邏輯或「邏輯」有關的談論實在有些離譜，我們在這裏不得不說幾句。

「邏輯是什麼」不是邏輯問題

在中國，「邏輯是什麼」或「什麼是邏輯」這類問題談的特別多，學生們也好奇。一位美國邏輯學家在訪問中國期間，曾應邀在某次學術討論會上做了報告。事後，有一次他和我通電話，談起那次會議。我問他與會者對他發言的討論情況，他回答說，沒什麼邏輯問題，基本上就是問「邏輯是什麼」。

學邏輯的人首先應該明白：「邏輯是什麼」這類問題都不是邏輯問題。如果我們去上數學課或物理課，或是去讀一篇數學論文或物理學論文，老師或作者會在那裏大談數學是什麼或物理學是什麼嗎？不會，至少通常不會。相反，他們會討論一些具體的數學或物理問題，會告訴我們如何解決這些問題；他們也會討論一些理論，會告訴我們這些理論如何解決若干類問題。相反，如果我們去上國內流行的哲學課或讀一篇哲學論文，遇到對具體哲學問題的討論的概率幾乎就是零。所以，從這樣的角度來看，邏輯學像科學（注：本講義中，「科學」指數學和被稱爲自然科學的那些學科。我們無意在這裏涉及科學哲學中關於數學是否科學的問題，也無意介入對類似問題的討論。自然，一旦數學是科學，當代邏輯學也應是科學，因爲無論是就對象還是就方法而言，當代邏輯學與數學的類似都不亞於任何其他被稱爲科學的學科。）而不像國內流行的哲學，因爲邏輯學研究各種各樣的具體的邏輯問題。

「邏輯是什麼」這類問題，當然可以討論。這樣的討論有兩種。一是隨便談談看法，二是認眞的學術討論。如果是隨便談看法，即使是外行來談，只要談的不是太離譜人們也不會去較眞，因爲任何人都可以有自己的看法。（注：“Few men think, yet all will have opinions?” — George Berkeley, Three Dialogues between Hylas and philonous, 1713.）認眞的學術討論則不同，它決不像外行或初學者想像的那麼簡單，而且即使討論者的態度是十二分的認眞，也未必能使人嚴肅認眞地對待他們的討論。這是因爲，要認眞討論「邏輯是什麼」這類問題，首先要熟悉邏輯，要有較全面的學識和較好的修養。倘若只讀了幾本邏輯敎科書，甚至連像樣的敎課書都沒好好讀過，那麼討論「邏輯是什麼」這類問題是不會得要領的，從而無法指望內行人認眞對待這樣的討論。

總有一些人，邏輯沒入門，卻偏偏熱衷於談論「邏輯是什麼」，「邏輯學有多少種」，「邏輯研究有幾個層面」和「邏輯學的發展方向」，等等。他們把外行話當「學術論文」寫，當「學術報告」講，甚至不惜誤人子弟也要把這些東西炒響做大。眞想學點邏輯的人要小心：這些東西只和「邏輯」這個名稱有關，和邏輯學的內容不沾邊。任何人把自己做的事稱作「對科學研究的貢獻」，都只是他個人的事；但如果以爲只要能炒響做大，內行們就不得不認眞對待，甚至不得不承認，那纔是典型的科學外行的一廂情願。

邏輯與「邏輯」的用法

有「專家」說，要想確定邏輯是什麼，就要看歷史上和現實中人們怎麼用「邏輯」這個詞，並聲稱只有這樣得出的看法纔是「客觀的」。於是，經過對「邏輯」用法的一番「考察」得出結論：邏輯除亞里士多德邏輯、數理邏輯和概率邏輯，還有方法論和知識論、非形式邏輯和辯證邏輯，共有五六種。

按說，當「專家」一本正經地談「學術」時，總不至於信口開河；可我們的「專家」實在不爭氣。單看結論就已令人大跌眼鏡，因爲僅憑常識也知道「邏輯」的用法遠不止這五六種。

用 google 搜索一下就有以下結果：當代邏輯（數理邏輯、古典邏輯、哲學邏輯、非古典邏輯）、形式邏輯、歸納邏輯、概率邏輯、傳統邏輯、發現的邏輯、辯證邏輯、非形式邏輯、自然語言邏輯、模糊邏輯、人工智能邏輯、中國古代邏輯、法律邏輯、經濟邏輯、商業邏輯、商務邏輯、資本邏輯、營銷邏輯、地產邏輯、自然邏輯、人文邏輯、社會邏輯、敎育邏輯、文學邏輯、歷史邏輯、藝術邏輯、審美邏輯、男性邏輯、女性邏輯、憤青邏輯、癡呆邏輯、行政邏輯、和諧邏輯、創新邏輯、文化邏輯、潛邏輯、足球邏輯、致富邏輯、運氣邏輯、統治邏輯、專制邏輯、官場邏輯、官僚邏輯、升官邏輯、軍閥邏輯、土匪邏輯、強盜邏輯、流氓邏輯、痞子邏輯、騙子邏輯、廁所邏輯，等等。

「邏輯」的諸多用法顯然無法對應於「專家」說的那五六種邏輯，這一事實不僅無法否認，而且與「專家」的前提和結論無法同世而立。所以，如果我們的「專家」不肯放棄他的前提或結論，那就只會讓自己落到全無邏輯的地步。（這也是「邏輯」的一種用法!）

外行人如何使用「邏輯」這個詞，邏輯學者通常沒必要認眞，因爲「邏輯」這個詞早被人們或有意或無意地濫用，在很多情況下與作爲一個學科的邏輯學沒什麼關係，正像「科學」這個詞的很多用法與科學沒什麼關係一樣。按說，內行人不在乎外行人對他們的學科怎麼說一一科學家不在乎哲學家怎麼定義科學就是很好的說明；那麼，我們的「邏輯專家」在界定邏輯學時，何以恰恰相反，求助於外行關於「邏輯」的說法呢？套用一句話：這種人其實是外行，或者裝作是外行。（二狗曰：「邏輯」有很多種，「邏輯學」也有很多種。）

邏輯與「習慣的說理方式」

地球是否圍繞着太陽轉？每個大於 1 的自然數是否都是某些素數的積？這些科學問題的答案和人們的習慣看法無關。同樣地，從「如果 $\varphi$ 則 $\chi$」和「如果 $\psi$ 則 $\chi$」是否可推出「如果 $\varphi$ 或 $\psi$ 那麼 $\chi$」，也和人們的說理習慣無關。邏輯區分好的說理和壞的說理，但不以人們習慣的說理方式爲根據。

記得曾有人主張「有些 $S$ 是 $P$」蘊涵「有些 $S$ 不是 $P$」，理由就是人們常這樣說理，比如從「有些學生遲到了」推岀「有些同學沒遲到」，等等。令人費解的是，這些人大都承認，從「所有 $S$ 是 $P$」可以「合理地」推出「有些 $S$ 是 $P$」（假定說「所有$S$ 是 $P$」時總有 $S$ 存在），卻看不出這樣一來，從「所有 $S$ 是 $P$」就可以「合理地」推出「有些 $S$ 不是 $P$」，於是可以「合理地」推出邏輯矛盾。把習慣的說理方式看作合理的說理方式，其結果只會是混亂。

近來更有人把文化問題裝扮成科學問題，宣稱存在不同的邏輯，其理由是不同文化中人們有不同的說理方式和習慣。按照這種人的說法，不僅中國人的說理方式和習慣與西方人的不同，漢族的說理方式和習慣與其他民族的也不同；所以中國有中國的邏輯，西方有西方的邏輯；漢族有漢族的邏輯，其他民族有其他民族的邏輯。同時，爲了表明這種「理論研究」有社會效益，還特意爲它插上「有助於各民族的相互了解」和「有利於社會發展」的標籤。

不同文化中，人們的確可以有不同的說理方式和習慣；但同一個文化中，人們照樣可以有不同的說理方式和習慣。倘若說理方式和習慣的不同眞能說明存在不同的邏輯，那麼，豈止是各國可以有各國的邏輯，或各民族可以有各民族的邏輯？各地區也可以有各地區的邏輯，各校又可以有各校的邏輯，甚至個人還可以有個人的邏輯——誰沒有自己的說理方式和習慣呢？這世界上有一類人，他們習慣的說理方式是「空着肚子說氣壯的話」，以自稱「永遠不會錯」爲這類氣壯話的典型。這能否說明存在一種與之相應的「邏輯」，進而也該對它做一番「研究」呢？

假如今天哪個文化圈裏的人習慣地認爲圓周率是 3，或習慣地認爲一萬乘以一萬就是無窮，那麼頭腦正常的人不會因此而聲稱存在不同的數學。假如昨天發現了某個遠離現代社會的原始部落，那裏的人都習慣地認爲太陽繞着地球轉，或認爲人是貓變來的，那麼頭腦正常的人也不會因此而聲稱存在不同的物理學或生物學。偏偏中國的哲學和邏輯學先天不足，後天失調，「不同說理方式和習慣導致不同邏輯」這類昏話，竟也可以被稱作學術研究而登堂入室。

當代邏輯、傳統邏輯和「普通人需要的邏輯」

這門課叫「符號邏輯」，取這個名字只是爲區別於其他邏輯課程，如「數理邏輯」等；但這些課程名稱的不同，並不意味着符號邏輯和數理邏輯是不同的邏輯。在國際主流邏輯學界，「符號邏輯」「數理邏輯」「形式邏輯」「當代邏輯」通常都是指同一個東西。

傳統的形式邏輯（在國內曾被稱爲「形式邏輯」，現在多被稱爲「普通邏輯」或「傳統邏輯」）是幼年的形式邏輯，它從根本上說只構成當代邏輯的一個很小的部分。儘管幼年的形式邏輯在人類文明史上有着不可磨滅的貢獻，但隨着科學的發展，它提供的邏輯觀念、理論和工具，相對於科學（尤其是數學）研究的需要來說，顯得越來越貧乏，越來越不足道。自弗雷格以來的當代邏輯，無論是就基礎的堅實還是就方法的完善來講，都大大超過了幼年的形式邏輯；而更重要的是，從當代邏輯研究中產生的新觀念和發現的新規律，爲科學的發展提供了更好的邏輯理論和工具。［Tarski,1941］用 20 世紀最傑出的邏輯學家哥德爾的話說：

數理邏輯不是別的，就是形式邏輯的準確和完備的表述。它有很不同的兩面。一方面，它是數學的一個部門，處理着類、關係、符號組合等等，而不是數、函數、幾何圖形等等。另一方面，它是先於一切科學的一門科學，包含着位於一切科學底層的觀念和原理。［Gödel,1944］

有些人總在抱怨：當代邏輯太技術化，太專業化了，越來越不適宜滿足日常思維的實際需求。他們舉出很多當代邏輯不考慮普通人需求的證據，如形式語言和數學方法等，還有很多當代邏輯課不受普通學生歡迎的故事。有些人甚至聲稱，數理邏輯的純技術化和數學化發展，已經在某種程度上對邏輯的存在構成了威脅。於是他們主張搞一種源於傳統邏輯而又適應普通人思維實際需要的「新邏輯」，稱之爲「批判性思維」或「非形式邏輯」。

「批判性思維」之類的東西，作爲一種初級邏輯的敎學模式，或者作爲關於初級邏輯的普及和日常應用的探索，是值得鼓勵的。在美國不少大學，「邏輯導論」課是通選課，雖俗稱「baby logic」，但仍有不少學生難以過關；而「批判性思維」課（如果有的話），俗稱「baby baby logic」，就是專爲這些學生開設的。國內不少學生甚至學者在邏輯性方面的欠缺是嚴重的，而普通的「邏輯導論」課又似乎對他們幫助不大；因而就邏輯的敎學和普及而言，我贊成借鑑甚至進口「批判性思維」這類課程。（二狗曰：批判性思維：foetus logic；邏輯導論：baby logic；經典數理邏輯：basic logic.）但是，就邏輯理論而言，「新邏輯」並不是新邏輯，因爲無論人們的願望是什麼，它尚未提供能與當代邏輯理論相比的邏輯理論。

初級邏輯的普及和日常應用問題，甚至當代邏輯的應用問題，都可以討論甚至應該重視；但面向大眾的邏輯課是一回事，邏輯理論研究是另一回事。這問題本來很簡單，就像文科學生的數學課，總不能和數學系的課一模一樣；但這決不意味着「文科數學」是有別於主流數學的另一種數學。其實，即使從應用角度來說，當代邏輯的主要目標也是爲理論研究、尤其是科學理論研究提供更好的邏輯理論和工具——它早已遠遠超出了「滿足普通人日常需要」的眼界。在這方面，邏輯學和其他科學一樣，其理論研究結果應該不是普通人一看就懂且馬上能用的。在科學的實際應用方面，普通人包括學生大概都有發言權；但倘若評價科學理論要以外行的好惡爲標準，科學理論問題要靠他們投票來解決，那麼科學就不再是科學了。

當代邏輯學家既不拒絕對新問題的探討，也不拒絕對現有理論的重新思考。惟其如此，纔會出現眾多的所謂新邏輯。不過，新邏輯的出現，不是靠拒絕當代邏輯的基本思想和方法，更不是靠知難而退式的「另起爐竈」。恰恰相反，這些新邏輯都是運用當代邏輯基本思想和方法的產物，進而逐步成爲當代邏輯的新分支。（注：這些分支數量之多，已使精通所有分支的「全才」成爲「歷史人物」。十多年前去世的 A. Church 傳說是最後一位「所有邏輯文章的評審員」，而這種說法顯然不是針對晚年的 Church 來說的。）任何人想再搞一套邏輯都可以，但要拿出能與主流理論競爭的理論。當眞要競爭，總不能比對手差太遠，起碼要知道對手做什麼，而不能像某些「$X$ 科學」的鼓吹者那樣，對眞正的科學一知半解，且所謂「競爭」也只限於對主流科學界的抱怨和基於非科學評價的煽情。

和任何科學一樣，邏輯學研究有大量人的參與。隨着學科的快速發展，除非是天才，不學習就要落後，落後嚴重的就會變成外行。說白了，即便是亞里士多德再世，如果他既不學當代邏輯又只能做他兩千年前做出的工作，那麼他也只是個亞氏邏輯專家，而不是當代的邏輯學家。這樣說似乎對亞氏不敬，但邏輯學科的發展和進步使亞式邏輯成爲歷史卻是事實。今天，只懂得畢達哥拉斯時代的數學的人不會被稱爲數學家，只懂得牛頓時代的物理學的人也不會被稱爲物理學家。根據同樣的道理，只懂得亞式邏輯的人，不會是當代的邏輯學家。如今，想要成爲邏輯學內行，學習當代邏輯是必由之路；而若想和當代邏輯競爭，學懂當代邏輯更是必要條件。

當代邏輯有很多分支，研究者文理各科都有，研究興趣也不一樣；但有一點是相同的，即都用形式語言和數學方法討論邏輯問題。對當代邏輯專業化和技術化的抱怨，主要是針對這種形式語言和數學方法的抱怨。

弗雷格曾把他的概念文字與日常語言的關係比作顯微鏡與眼睛的關係。［Frege,1879］眼睛的適用範圍和適應環境的靈活性遠遠高於顯微鏡，然而，一旦科學研究需要更敏銳的分辨能力，眼睛就立刻讓位於顯微鏡。儘管後者在滿足普通人的實際需要方面毫無用武之地，但它不應因此而受到指責。研究方法上的改進推動科學的進步，甚至比孤立的個別發現更加重要，這在科學界已是共識。恰恰是形式語言和數學方法的運用，使人們對眞假、邏輯蘊涵、演繹、證明、一致性和公理系統等的認識有了空前的提高，也使邏輯學最終走出了它的幼年時期而與其他科學站到了一起，併爲其他科學的理論研究提供了大量的邏輯理論和工具。在這種情況下，抱怨形式語言和數學方法不滿足日常思維的需求，就像抱怨顯微鏡無助於提高普通人對日常現象的觀察能力；這不僅不得要領，更清楚地表明抱怨者沒有跟上邏輯學科的發展，其「邏輯觀」還停留在弗雷格之前的某個年代。

當然，這並不是說當代邏輯對普通人的工作和生活完全沒有影響。與各種科學理論研究一樣，當代邏輯要繞很多彎子纔能與普通人聯繫上。比如，我們都知道，個人電腦和計算機網絡對普通人工作和生活的影響越來越大；而當代邏輯通過個人電腦和計算機網絡就聯繫到我們的工作和生活，只不過要兜個圈子：它先聯繫到計算機科學，再經後者的理論研究聯繫到它的應用研究和技術研究，最後再經過具體硬件和軟件的開發、生產和銷售等中介，纔聯繫到個人電腦和計算機網絡，纔聯繫到我們的工作和生活。儘管當代邏輯是計算機科學的基礎理論之一，但使用個人電腦和計算機網絡的普通人，卻不需要懂當代邏輯（即使普通的程序員也不需要懂多少）。科學就是這樣：它不要求所有的人都懂，卻可以使所有的人受益。

如果讀者願意學點當代邏輯，又做好了克服困難的思想準備，那麼我們的「邏輯旅程」就可以開始了。不過，當代邏輯從弗雷格算起雖只有一百多年時間，但內容豐富，分支很多，而且發展很快。讀者在這裏能夠看到的，只是它最淺顯的一部分。這份講義雖然長達幾百頁，一旦學懂了，大概就只剩幾十頁了。

The article was recently updated on Saturday, March 18, 2023, 14:28:36 by 王小花.