集合：属性、元素、外延

Extensionality

A set is a collection of objects, considered {as} a single object. The objects making up the set are called elements or members of the set. If $x$ is an element of a set $a$, we write $x \in a$; if not, we write $x \notin a$. The set which has no elements is called the empty set and denoted “$\varnothing$’'.

It does not matter how we specify the set, or how we order its elements, or indeed how many times we count its elements. All that matters are what its elements are. We codify this in the following principle.

Extensionality licenses some notation. In general, when we have some objects $a_{1}, \cdots, a_{n}$, then $\lbrace a_{1}, \cdots, a_{n}\rbrace$ is the set whose elements are $a_1, \ldots, a_n$. We emphasise the word “the’’, since extensionality tells us that there can be only one such set. Indeed, extensionality also licenses the following:

$$\lbrace a, a, b \rbrace = \lbrace a, b \rbrace = \lbrace b,a \rbrace. $$

This delivers on the point that, when we consider sets, we don’t care about the order of their elements, or how many times they are specified.

Frequently we’ll specify a set by some property that its elements share. We’ll use the following shorthand notation for that: {$x: \varphi(x)$}, where the $\varphi(x)$ stands for the property that $x$ has to have in order to be counted among the elements of the set.

We read the notation on the right as “the set of $x$’s such that $x$ is perfect and $0 \leqslant x \leqslant 10$’’. The identity here confirms that, when we consider sets, we don’t care about how they are specified. And, more generally, extensionality guarantees that there is always only one set of $x$’s such that $\varphi(x)$. So, extensionality justifies calling $\lbrace x: \varphi(x)\rbrace$ the set of $x$’s such that $\varphi(x)$.

Extensionality gives us a way for showing that sets are identical: to show that $A = B$, show that whenever $x \in A$ then also $x \in B$, and whenever $y \in B$ then also $y \in A$.

Problem 1.0
Prove that there is at most one empty set, i.e., show that if $A$ and $B$ are sets without elements, then $A = B$.

Subsets and Power Sets

We will often want to compare sets. And one obvious kind of comparison one might make is as follows: everything in one set is in the other too. This situation is sufficiently important for us to introduce some new notation.

Extensionality gives a criterion of identity for sets: $A = B$ iff every element of $A$ is also an element of $B$ and vice versa. The definition of “subset’’ defines $A \subseteq B$ precisely as the first half of this criterion: every element of $A$ is also an element of $B$. Of course the definition also applies if we switch $A$ and $B$: that is, $B \subseteq A$ iff every element of $B$ is also an element of $A$. And that, in turn, is exactly the “vice versa’’ part of extensionality. In other words, extensionality entails that sets are equal iff they are subsets of one another.

Now is also a good opportunity to introduce some further bits of helpful notation. In defining when $A$ is a subset of $B$ we said that “every element of $A$ is $\cdots$,’’ and filled the “$\cdots$’’ with “an element of $B$’’. But this is such a common shape of expression that it will be helpful to introduce some formal notation for it.

Using this notation, we can say that $A \subseteq B$ iff $(\forall x \in A)x \in B$.

Now we move on to considering a certain kind of set: the set of all subsets of a given set.

Problem 1.1 List all subsets of $\lbrace a, b, c, d\rbrace$.

Problem 1.2 Show that if $A$ has $n$ elements, then $\mathscr{P}(A)$ has $2^n$ elements.

Some Important Sets

Unions and Intersections

We introduced definitions of sets by abstraction, i.e., definitions of the form $\lbrace x: \phi(x)\rbrace $. Here, we invoke some property $\phi$, and this property can mention sets we’ve already defined. So for instance, if $A$ and $B$ are sets, the set $\lbrace x: x \in A \lor x \in B\rbrace $ consists of all those objects which are elements of either $A$ or $B$, i.e., it’s the set that combines the elements of $A$ and $B$. We can visualize this as in Figure 1.0, where the highlighted area indicates the bb>elements of the two sets $A$ and $B$ together.

This operation on sets—combining them—is very useful and common, and so we give it a formal name and a symbol.

Problem 1.3
Prove that if $A \subseteq B$, then $A \cup B = B$.

We can also consider a “dual’’ operation to union. This is the operation that forms the set of all elements that are elements of $A$ and are also elements of $B$. This operation is called intersection, and can be depicted as in Figure 1.1.

Problem 1.4
Prove rigorously that if $A \subseteq B$, then $A \cap B = A$.

We can also form the union or intersection of more than two sets. An elegant way of dealing with this in general is the following: suppose you collect all the sets you want to form the union (or intersection) of into a single set. Then we can define the union of all our original sets as the set of all objects which belong to at least one element of the set, and the intersection as the set of all objects which belong to every element of the set.

Problem 1.3
Show that if $A$ is a set and $A \in B$, then $A \subseteq \bigcup B$.

We could also do the same for a sequence of sets $A_1$, $A_2, \cdots$,

$$ \begin{aligned} \bigcup_i A_i & = \{x: x \text{ belongs to one of the } A_i\}\\ \bigcap_i A_i & = \{x: x \text{ belongs to every } A_i\}. \end{aligned} $$

When we have an index of sets, i.e., some set $I$ such that we
are considering $A_i$ for each $i \in I$, we may also use these
abbreviations:

$$ \begin{aligned} \bigcup_{i \in I} A_i & = \bigcup \{A_i: i \in I\}\\ \bigcap_{i \in I} A_i & = \bigcap\{A_i: i \in I\} \end{aligned} $$

Finally, we may want to think about the set of all elements in $A$ which are not in $B$. We can depict this as in Figure 1.2.

Problem 1.3
Prove that if $A \subsetneq B$, then $B \setminus A \neq \varnothing$.

Pairs, Tuples, Cartesian Products

It follows from extensionality that sets have no order to their elements. So if we want to represent order, we use ordered pairs $⟨x, y⟩$. In an unordered pair $\lbrace x, y\rbrace $, the order does not matter: $\lbrace x, y\rbrace = \lbrace y, x\rbrace $. In an ordered pair, it does: if $x \neq y$, then $⟨x, y⟩ \neq ⟨y, x⟩$.

How should we think about ordered pairs in set theory? Crucially, we want to preserve the idea that ordered pairs are identical iff they share the same first element and share the same second element, i.e.: $$⟨a, b⟩= ⟨c, d⟩\text{ iff both }a = c \text{ and }b=d.$$ We can define ordered pairs in set theory using the Wiener-Kuratowski definition.

Problem 1.3
Using Definition 1.9, prove that $⟨a, b⟩= ⟨c, d⟩$ iff both $a = c$ and $b=d$.

Having fixed a definition of an ordered pair, we can use it to define further sets. For example, sometimes we also want ordered sequences of more than two objects, e.g., triples $⟨x, y, z⟩$, quadruples $⟨x, y, z, u⟩$, and so on. We can think of triples as special ordered pairs, where the first element is itself an ordered pair: $⟨x, y, z⟩$ is $⟨⟨x, y⟩,z⟩$. The same is true for quadruples: $⟨x,y,z,u⟩$ is $⟨⟨⟨x,y⟩,z⟩,u⟩$, and so on. In general, we talk of ordered $n$-tuples $⟨x_1, \cdots, x_n⟩$.

Certain sets of ordered pairs, or other ordered $n$-tuples, will be useful.

Problem 1.3
List all elements of $\lbrace 1, 2, 3\rbrace ^3$.

命題 1.1 之證明
For every element $x$ in $A$, there are $m$ elements of the form $⟨x, y⟩ \in A \times B$. Let $B_x = \lbrace ⟨x, y⟩: y \in B\rbrace $. Since whenever $x_1 \neq x_2$, $⟨x_1, y⟩ \neq ⟨x_2, y⟩$, $B_{x_1} \cap B_{x_2} = \varnothing$. But if $A = \lbrace x_1, \cdots, x_n\rbrace $, then $A \times B = B_{x_1} \cup \cdots \cup B_{x_n}$, and so has $n\cdot m$ elements.
To visualize this, arrange the elements of $A \times B$ in a grid:

\[ \begin{array}{rcccc} B_{x_1} = & \{⟨x_1, y_1⟩ & ⟨x_1, y_2⟩ & \cdots & ⟨x_1, y_m⟩\}\\ B_{x_2} = & \{⟨x_2, y_1⟩ & ⟨x_2, y_2⟩ & \cdots & ⟨x_2, y_m⟩\}\\ \vdots & & \vdots\\ B_{x_n} = & \{⟨x_n, y_1⟩ & ⟨x_n, y_2⟩ & \cdots & ⟨x_n, y_m⟩\} \end{array} \]

Since the $x_i$ are all different, and the $y_j$ are all different, no two of the pairs in this grid are the same, and there are $n\cdot m$ of them.

Problem 1.3
Show, by induction on $k$, that for all $k \ge 1$, if $A$ has $n$ elements, then $A^k$ has $n^k$ elements.

Russell’s Paradox

Extensionality licenses the notation $\lbrace x: \phi(x)\rbrace $, for the set of $x$’s such that $\phi(x)$. However, all that extensionality really licenses is the following thought. If there is a set whose members are all and only the $\phi$’s, then there is only one such set. Otherwise put: having fixed some $\phi$, the set $\lbrace x: \phi(x)\rbrace $ is unique, if it exists.

But this conditional is important! Crucially, not every property lends itself to comprehension. That is, some properties do not define sets. If they all did, then we would run into outright contradictions. The most famous example of this is Russell’s Paradox.

Sets may be elements of other sets—for instance, the power set of a set $A$ is made up of sets. And so it makes sense to ask or investigate whether a set is an element of another set. Can a set be a member of itself? Nothing about the idea of a set seems to rule this out. For instance, if all sets form a collection of objects, one might think that they can be collected into a single set—the set of all sets. And it, being a set, would be an element of the set of all sets.

Russell’s Paradox arises when we consider the property of not having itself as an element, of being non-self-membered. What if we suppose that there is a set of all sets that do not have themselves as an element? Does $$R = \lbrace x: x \notin x\rbrace$$ exist? It turns out that we can prove that it does not.

Theorem 1.0 之證明
For reductio, suppose that $R = \lbrace x: x \notin x\rbrace $ exists. Then $R \in R$ iff $R \notin R$, since sets are extensional. But this is a contradicion.

Let’s run through the proof that no set $R$ of non-self-membered sets can exist more slowly. If $R$ exists, it makes sense to ask if $R \in R$ or not—it must be either $\in R$ or $\notin R$. Suppose the former is true, i.e., $R \in R$. $R$ was defined as the set of all sets that are not elements of themselves, and so if $R \in R$, then $R$ does not have this defining property of $R$. But only sets that have this property are in $R$, hence, $R$ cannot be an element of $R$, i.e., $R \notin R$. But $R$ can’t both be and not be an element of $R$, so we have a contradiction.

Since the assumption that $R \in R$ leads to a contradiction, we have $R \notin R$. But this also leads to a contradiction! For if $R \notin R$, it does have the defining property of $R$, and so would be an element of $R$ just like all the other non-self-membered sets. And again, it can’t both not be and be an element of $R$.

How do we set up a set theory which avoids falling into Russell’s Paradox, i.e., which avoids making the inconsistent claim that $R = \lbrace x: x \notin x\rbrace $ exists? Well, we would need to lay down axioms which give us very precise conditions for stating when sets exist (and when they don’t).

The set theory sketched in this chapter doesn’t do this. It’s genuinely naïve. It tells you only that sets obey extensionality and that, if you have some sets, you can form their union, intersection, etc. It is possible to develop set theory more rigorously than this.

关系：集合上的结构

Relations as Sets

In §1.0.2（P.19）, we mentioned some important sets: $\mathbb{N}$, $\mathbb{Z}$, $\mathbb{Q}$, $\mathbb{R}$. You will no doubt remember some interesting relations between the elements of some of these sets. For instance, each of these sets has a completely standard order relation on it. There is also the relation is identical with that every object bears to itself and to no other thing. There are many more interesting relations that we’ll encounter, and even more possible relations. Before we review them, though, we will start by pointing out that we can look at relations as a special sort of set.

For this, recall two things from §1.0.4（P.22）. First, recall the notion of a ordered pair: given $a$ and $b$, we can form $⟨a, b⟩$. Importantly, the order of elements does matter here. So if $a \neq b$ then $⟨a, b⟩ \neq ⟨b, a⟩$. (Contrast this with unordered pairs, i.e., $2$-element sets, where $\lbrace a, b\rbrace =\lbrace b, a\rbrace $.) Second, recall the notion of a Cartesian product: if $A$ and $B$ are sets, then we can form $A \times B$, the set of all pairs $⟨x, y⟩$ with $x \in A$ and $y \in B$. In particular, $A^{2}= A \times A$ is the set of all ordered pairs from $A$.

Now we will consider a particular relation on a set: the $<$-relation on the set $\mathbb{N}$ of natural numbers. Consider the set of all pairs of numbers $⟨n, m⟩$ where $n < m$, i.e., $$R= \lbrace ⟨n, m⟩: n, m \in \mathbb{N} \text{ and } n < m \rbrace.$$ There is a close connection between $n$ being less than $m$, and the pair $⟨n, m⟩$ being a member of $R$, namely: $$n < m \text{ iff }⟨n, m⟩ \in R.$$ Indeed, without any loss of information, we can consider the set $R$ to be the $<$-relation on $\mathbb{N}$.

In the same way we can construct a subset of $\mathbb{N}^{2}$ for any relation between numbers. Conversely, given any set of pairs of numbers $S \subseteq \mathbb{N}^{2}$, there is a corresponding relation between numbers, namely, the relationship $n$ bears to $m$ if and only if $⟨n, m⟩ \in S$. This justifies the following definition:

Although orders and identity are important and natural relations, it should be emphasized that according to our definition any subset of $A^{2}$ is a relation on $A$, regardless of how unnatural or contrived it seems. In particular, $\varnothing$ is a relation on any set (the empty relation, which no pair of elements bears), and $A^{2}$ itself is a relation on $A$ as well (one which every pair bears), called the universal relation. But also something like $E=\lbrace ⟨n, m⟩: n>5 \text{ or } m \times n \ge 34\rbrace $ counts as a relation.

Problem 1.10
List the elements of the relation $\subseteq$ on the set $\mathscr{P}({\lbrace a, b, c\rbrace })$.

Philosophical Reflections

In §1.1.0（P.26）, we defined relations as certain sets. We should pause and ask a quick philosophical question: what is such a definition doing? It is extremely doubtful that we should want to say that we have discovered some metaphysical identity facts; that, for example, the order relation on $\mathbb{N}$ turned out to be the set $R= \lbrace ⟨n,m⟩: n, m \in \mathbb{N}\text{ and } n < m\rbrace $ we defined in §1.1.0（P.26）. Here are three reasons why.

First: in Definition 1.9, we defined $⟨a, b⟩ = \lbrace \lbrace a\rbrace , \lbrace a, b\rbrace \rbrace $. Consider instead the definition $\lVert a, b\rVert = \lbrace \lbrace b\rbrace , \lbrace a, b\rbrace \rbrace = ⟨b,a⟩$. When $a \neq b$, we have that $⟨a, b⟩ \neq \lVert a,b\rVert$. But we could equally have regarded $\lVert a,b\rVert$ as our definition of an ordered pair, rather than $⟨a,b⟩$. Both definitions would have worked equally well. So now we have two equally good candidates to “be’’ the order relation on the natural numbers, namely:

$$ \begin{aligned} R &= \{⟨n,m⟩: n, m \in \mathbb{N} \text{ and }n < m\}\\ S &= \{\lVert n,m\rVert: n, m \in \mathbb{N} \text{ and }n < m\}. \end{aligned} $$

Since $R \neq S$, by extensionality, it is clear that they cannot both be identical to the order relation on $\mathbb{N}$. But it would just be arbitrary, and hence a bit embarrassing, to claim that $R$ rather than $S$ (or vice versa) is the ordering relation, as a matter of fact. (This is a very simple instance of an argument against set-theoretic reductionism which Benacerraf made famous in 1965. We will revisit it several times.)

Second: if we think that every relation should be identified with a set, then the relation of set-membership itself, $\in$, should be a particular set. Indeed, it would have to be the set $\lbrace ⟨x,y⟩: x \in y\rbrace $. But does this set exist? Given Russell’s Paradox, it is a non-trivial claim that such a set exists. In fact, it is possible to develop set theory in a rigorous way as an axiomatic theory. In this theory, it will be provable that there is no set of all sets. So, even if some relations can be treated as sets, the relation of set-membership will have to be a special case.

Third: when we “identify’’ relations with sets, we said that we would allow ourselves to write $Rxy$ for $⟨x,y⟩ \in R$. This is fine, provided that the membership relation, “$\in$’’, is treated as a predicate. But if we think that “$\in$’’ stands for a certain kind of set, then the expression “$⟨x,y⟩ \in R$’’ just consists of three singular terms which stand for sets: “$⟨x,y⟩$’’, “$\in$’’, and “$R$’’. And such a list of names is no more capable of expressing a proposition than the nonsense string: “the cup penholder the table’’. Again, even if some relations can be treated as sets, the relation of set-membership must be a special case. (This rolls together a simple version of Frege’s concept horse paradox, and a famous objection that Wittgenstein once raised against Russell.)

So where does this leave us? Well, there is nothing wrong with our saying that the relations on the numbers are sets. We just have to understand the spirit in which that remark is made. We are not stating a metaphysical identity fact. We are simply noting that, in certain contexts, we can (and will) treat (certain) relations as certain sets.

Special Properties of Relations

Some kinds of relations turn out to be so common that they have been given special names. For instance, $\leqslant$ and $\subseteq$ both relate their respective domains (say, $\mathbb{N}$ in the case of $\leqslant$ and $\mathscr{P}({A})$ in the case of $\subseteq$) in similar ways. To get at exactly how these relations are similar, and how they differ, we categorize them according to some special properties that relations can have. It turns out that (combinations of) some of these special properties are especially important: orders and equivalence relations.

In a symmetric relation, $Rxy$ and $Ryx$ always hold together, or neither holds. In an anti-symmetric relation, the only way for $Rxy$ and $Ryx$ to hold together is if $x = y$. Note that this does not require that $Rxy$ and $Ryx$ holds when $x = y$, only that it isn’t ruled out. So an anti-symmetric relation can be reflexive, but it is not the case that every anti-symmetric relation is reflexive. Also note that being anti-symmetric and merely not being symmetric are different conditions. In fact, a relation can be both symmetric and anti-symmetric at the same time (e.g., the identity relation is).

Problem 1.11
Give examples of relations that are (a) reflexive and symmetric but not transitive, (b) reflexive and anti-symmetric, (c) anti-symmetric, transitive, but not reflexive, and (d) reflexive, symmetric, and transitive. Do not use relations on numbers or sets.

Note that if $A \neq \varnothing$, then no irreflexive relation on $A$ is reflexive and every asymmetric relation on $A$ is also anti-symmetric. However, there are $R \subseteq A^2$ that are not reflexive and also not irreflexive, and there are anti-symmetric relations that are not asymmetric.

Equivalence Relations

The identity relation on a set is reflexive, symmetric, and
transitive. Relations $R$ that have all three of these properties are very
common.

Equivalence relations give rise to the notion of an equivalence class. An equivalence relation “chunks up’’ the domain into different partitions. Within each partition, all the objects are related to one another; and no objects from different partitions relate to one another. Sometimes, it’s helpful just to talk about these partitions directly. To that end, we introduce a definition:

The next result vindicates the definition of an equivalence class, in proving that the equivalence classes are indeed the partitions of $A$:

命題 1.2 之證明
For the left-to-right direction, suppose $Rxy$, and let $z \in [x]_R$. By definition, then, $Rxz$. Since $R$ is an equivalence relation, $Ryz$. (Spelling this out: as $Rxy$ and $R$ is symmetric we have $Ryx$, and as $Rxz$ and $R$ is transitive we have $Ryz$.) So $z \in [y]_R$. Generalising, $[x]_R \subseteq [y]_R$. But exactly similarly, $[y]_R \subseteq [x]_R$. So $[x]_R = [y]_R$, by extensionality.
For the right-to-left direction, suppose $[x]_R = [y]_R$. Since $R$ is reflexive, $Ryy$, so $y \in [y]_R$. Thus also $y \in [x]_R$ by the assumption that $[x]_R = [y]_R$. So $Rxy$.

Problem 1.12
Show that $\equiv_n$ is an equivalence relation, for any $n \in \mathbb{N}$, and that ${\mathbb{N}/}_{{\equiv}_n}$ has exactly $n$ members.

Orders

Many of our comparisons involve describing some objects as being “less than’’, “equal to’’, or “greater than’’ other objects, in a certain respect. These involve order relations. But there are different kinds of order relations. For instance, some require that any two objects be comparable, others don’t. Some include identity (like $\leqslant$) and some exclude it (like $<$). It will help us to have a taxonomy here.

Every linear order is also a partial order, and every partial order is also a preorder, but the converses don’t hold.

Any strict order $R$ on $A$ can be turned into a partial order by adding the diagonal Id$_{A}$, i.e., adding all the pairs $⟨x, x⟩$. (This is called the reflexive closure of $R$.) Conversely, starting from a partial order, one can get a strict order by removing Id$_A$. These next two results make this precise.

命題 1.3 之證明

1. Suppose $R$ is a strict order, i.e., $R \subseteq A^2$ and $R$ is irreflexive, asymmetric, and transitive. Let $R^+ = R \cup Id_A$. We have to show that $R^+$ is reflexive, antisymmetric, and transitive.
2. $R^+$ is clearly reflexive, since $⟨x, x⟩ \in Id_A \subseteq R^+$ for all $x \in A.$
3. To show $R^+$ is antisymmetric, suppose for reductio that $R^+xy$ and $R^+yx$ but $x \neq y$. Since $⟨x,y⟩ \in R \cup Id_X$, but $⟨x, y⟩ \notin Id_X$, we must have $⟨x, y⟩ \in R$, i.e., $Rxy$. Similarly, $Ryx$. But this contradicts the assumption that $R$ is asymmetric.
4. To establish transitivity, suppose that $R^+xy$ and $R^+yz$. If both $⟨x, y⟩ \in R$ and $⟨y,z⟩ \in R$, then $⟨x, z⟩ \in R$ since $R$ is transitive. Otherwise, either $⟨x, y⟩ \in Id_X$, i.e., $x = y$, or $⟨y, z⟩ \in Id_X$, i.e., $y = z$. In the first case, we have that $R^+yz$ by assumption, $x = y$, hence $R^+xz$. Similarly in the second case. In either case, $R^+xz$, thus, $R^+$ is also transitive.
5. Concerning the “moreover’’ clause, suppose $R$ is a total order, i.e., that $R$ is connected. So for all $x \neq y$, either $Rxy$ or $Ryx$, i.e., either $⟨x, y⟩ \in R$ or $⟨y, x⟩ \in R$. Since $R \subseteq R^+$, this remains true of $R^+$, so $R^+$ is connected as well.

命題 1.4 之證明
This is left as an exercise.

Problem 1.4
Give a proof of Proposition 1.4.

The following simple result which establishes that total orders satisfy an extensionality-like property:

命題 1.5 之證明
Suppose $(\forall x \in A)(x < a \leftrightarrow x < b)$. If $a < b$, then $a < a$, contradicting the fact that $<$ is irreflexive; so $a \nless b$. Exactly similarly, $b \nless a$. So $a = b$, as $<$ is connected.

Graphs

A graph is a diagram in which points—called “nodes’’ or “vertices’’ (plural of “vertex’’)—are connected by edges. Graphs are a ubiquitous tool in discrete mathematics and in computer science. They are incredibly useful for representing, and visualizing, relationships and structures, from concrete things like networks of various kinds to abstract structures such as the possible outcomes of decisions. There are many different kinds of graphs in the literature which differ, e.g., according to whether the edges are directed or not, have labels or not, whether there can be edges from a node to the same node, multiple edges between the same nodes, etc. Directed graphs have a special connection to relations.

According to our definition, a graph just is a set together with a relation on that set. Of course, when talking about graphs, it’s only natural to expect that they are graphically represented: we can draw a graph by connecting two vertices $v_1$ and $v_2$ by an arrow iff $⟨v_1, v_2⟩ \in E$. The only difference between a relation by itself and a graph is that a graph specifies the set of vertices, i.e., a graph may have isolated vertices. The important point, however, is that every relation $R$ on a set $X$ can be seen as a directed graph $⟨X, R⟩$, and conversely, a directed graph $⟨V, E⟩$ can be seen as a relation $E \subseteq V^2$ with the set $V$ explicitly specified.

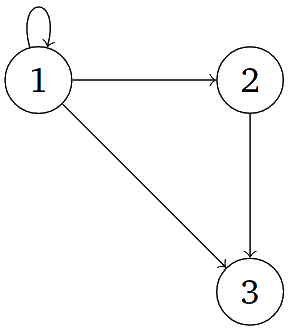
Problem 1.14
Consider the less-than-or-equal-to relation $\leqslant$ on the set $\lbrace 1, 2, 3, 4\rbrace $ as a graph and draw the corresponding diagram.

Operations on Relations

It is often useful to modify or combine relations. In
Proposition1.3（P.32）, we considered the union
of relations, which is just the union of two relations considered as
sets of pairs. Similarly, in Proposition1.4（P.33）,
we considered the relative difference of relations. Here are some
other operations we can perform on relations.

Problem 1.15
Show that the transitive closure of $R$ is in fact transitive.

函数：关系之特例

Basics

A function is a map which sends each element of a given set to a specific element in some (other) given set. For instance, the operation of adding $1$ defines a function: each number $n$ is mapped to a unique number $n+1$.

More generally, functions may take pairs, triples, etc., as inputs and returns some kind of output. Many functions are familiar to us from basic arithmetic. For instance, addition and multiplication are functions. They take in two numbers and return a third.

In this mathematical, abstract sense, a function is a black box: what matters is only what output is paired with what input, not the method for calculating the output.

The diagram in Figure 1.3 may help to think about functions. The ellipse on the left represents the function’s domain; the ellipse on the right represents the function’s codomain; and an arrow points from an argument in the domain to the corresponding value in the codomain.

We can define functions by specifying in some precise way what the
value of the function is for every possible argment. Different ways of
doing this are by giving a formula, describing a method for computing
the value, or listing the values for each argument. However functions
are defined, we must make sure that for each argment we specify one,
and only one, value.

We just considered two functions, $f$ and $g$, with different definitions. However, these are the same function. After all, for any natural number $n$, we have that $f(n) = n+1 = n+2-1 = g(n)$. Otherwise put: our definitions for $f$ and $g$ specify the same mapping by means of different equations. Implicitly, then, we are relying upon a principle of extensionality for functions, $$\text{if }\forall x, f(x) = g(x)\text{, then }f = g$$ provided that $f$ and $g$ share the same domain and codomain.

Kinds of Functions

It will be useful to introduce a kind of taxonomy for some of the kinds of functions which we encounter most frequently.

To start, we might want to consider functions which have the property that every member of the codomain is a value of the function. Such functions are called surjective, and can be pictured as in Figure 1.4.

If you want to show that $f$ is a surjection, then you need to show that every object in $f$’s codomain is the value of $f(x)$ for some input $x$.

Note that any function induces a surjection. After all, given a function $f \colon A \to B$, let $f’ \colon A \to \text{ran}(f)$ be defined by $f’(x) = f(x)$. Since $\text{ran}(f)$ is defined as $\lbrace f(x) \in B: x \in A\rbrace$, this function $f’$ is guaranteed to be a surjection.

Now, any function maps each possible input to a unique output. But there are also functions which never map different inputs to the same outputs. Such functions are called injective, and can be pictured as in Figure 1.5.

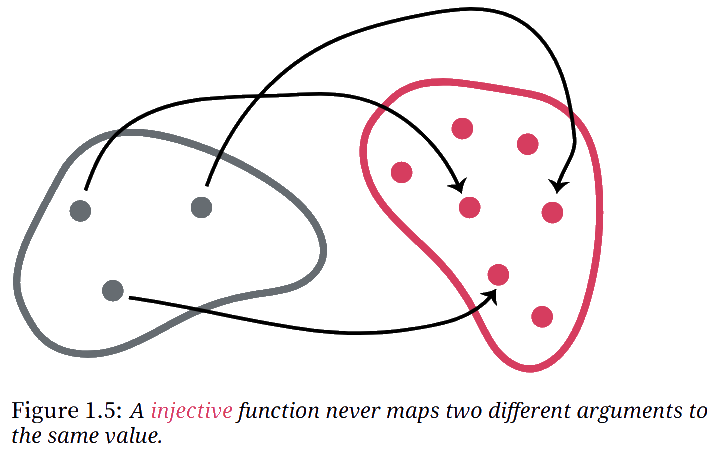
If you want to show that $f$ is an injection, you need to show that for any elements $x$ and $y$ of $f$’s domain, if $f(x)=f(y)$, then $x=y$.

Often enough, we want to consider functions which are both injective and surjective. We call such functions bijective. They look like the function pictured in Figure 1.6. bijections are also sometimes called one-to-one correspondences, since they uniquely pair elements of the codomain with elements of the domain.

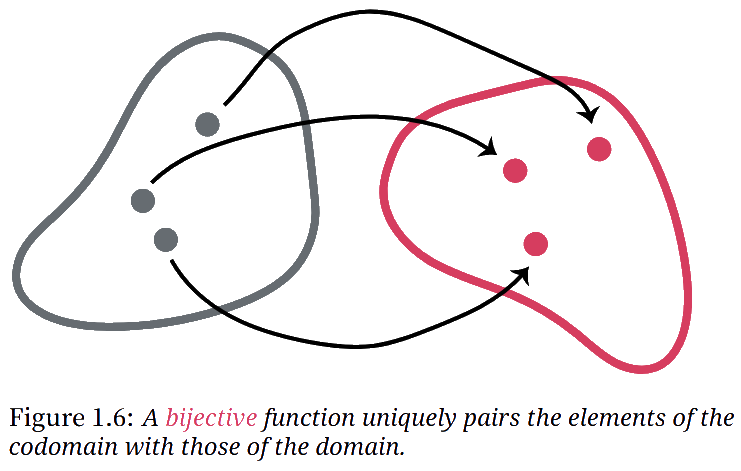
Functions as Relations

A function which maps elements of $A$ to elements of $B$ obviously defines a relation between $A$ and $B$, namely the relation which holds between $x$ and $y$ iff $f(x) = y$. In fact, we might even—if we are interested in reducing the building blocks of mathematics for instance—identify the function $f$ with this relation, i.e., with a set of pairs. This then raises the question: which relations define functions in this way?

The graph of a function is uniquely determined, by extensionality. Moreover, extensionality (on sets) will immediate vindicate the implicit principle of extensionality for functions, whereby if $f$ and $g$ share a domain and codomain then they are identical if they agree on all values.

Similarly, if a relation is “functional’’, then it is the graph of a function.

命題 1.6 之證明
Suppose there is a $y$ such that $Rxy$. If there were another $z \neq y$ such that $Rxz$, the condition on $R$ would be violated. Hence, if there is a $y$ such that $Rxy$, this $y$ is unique, and so $f$ is well-defined. Obviously, $R_f = R$.

Every function $f\colon A \to B$ has a graph, i.e., a relation on $A \times B$ defined by $f(x) = y$. On the other hand, every relation $R \subseteq A \times B$ with the properties given in Proposition 1.6 is the graph of a function $f \colon A \to B$. Because of this close connection between functions and their graphs, we can think of a function simply as its graph. In other words, functions can be identified with certain relations, i.e., with certain sets of tuples. Note, though, that the spirit of this “identification’’ is as in §1.1.1（P.28）: it is not a claim about the metaphysics of functions, but an observation that it is convenient to treat functions as certain sets. One reason that this is so convenient, is that We can now consider performing similar operations on functions as we performed on relations (see §1.1.6（P.34）). In particular:

It follows from these definition that $\text{ran}(f) = f[\text{dom}(f)]$, for any function $f$. These notions are exactly as one would expect, given the definitions in §1.1.6（P.34）and our identification of functions with relations. But two other operations—inverses and relative products—require a little more detail. We will provide that in the §1.2.3（P.41）and §1.2.4（P.42）.

Inverses of Functions

We think of functions as maps. An obvious question to ask about functions, then, is whether the mapping can be “reversed.’’ For instance, the successor function $f(x) = x + 1$ can be reversed, in the sense that the function $g(y) = y - 1$ “undoes’’ what $f$ does.

But we must be careful. Although the definition of $g$ defines a function $\mathbb{Z} \to \mathbb{Z}$, it does not define a function $\mathbb{N} \to \mathbb{N}$, since $g(0) \notin \mathbb{N}$. So even in simple cases, it is not quite obvious whether a function can be reversed; it may depend on the domain and codomain.

This is made more precise by the notion of an inverse of a function.

If $f$ has an inverse $g$, we often write $f^{-1}$ instead of $g$.

Now we will determine when functions have inverses. A good candidate for an inverse of $f\colon A \to B$ is $g\colon B \to A$ “defined by’’ $$g(y) = \text{“the’’ $x$ such that $f(x) = y$.}$$ But the scare quotes around “defined by’’ (and “the’’) suggest that this is not a definition. At least, it will not always work, with complete generality. For, in order for this definition to specify a function, there has to be one and only one $x$ such that $f(x) = y$—the output of $g$ has to be uniquely specified. Moreover, it has to be specified for every $y \in B$. If there are $x_1$ and $x_2 \in A$ with $x_1 \neq x_2$ but $f(x_1) = f(x_2)$, then $g(y)$ would not be uniquely specified for $y = f(x_1) = f(x_2)$. And if there is no $x$ at all such that $f(x) = y$, then $g(y)$ is not specified at all. In other words, for $g$ to be defined, $f$ must be both injective and surjective.

命題 1.7 之證明
Exercise.

Problem 1.16
Prove Proposition 1.7. That is, show that if $f\colon A \to B$ is bijective, an inverse $g$ of $f$ exists. You have to define such a $g$, show that it is a function, and show that it is an inverse of $f$, i.e., $f(g(y)) = y$ and $g(f(x)) = x$ for all $x \in A$ and $y \in B$.

However, there is a slightly more general way to extract inverses. We saw in §1.2.1（P.37）that every function $f$ induces a surjection $f’ \colon A \to \text{ran}(f)$ by letting $f’(x) = f(x)$ for all $x \in A$. Clearly, if $f$ is an injection, then $f’$ is a bijection, so that it has a unique inverse by Proposition 1.7. By a very minor abuse of notation, we sometimes call the inverse of $f’$ simply “the inverse of $f$.''

Problem 1.17
Show that if $f\colon A \to B$ has an inverse $g$, then $f$ is bijective.

命題 1.8 之證明
Exercise.

Problem 1.18
Prove Proposition 1.8. That is, show that if $g\colon B \to A$ and $g’\colon B \to A$ are inverses of $f\colon A \to B$, then $g = g’$, i.e., for all $y \in B$, $g(y) = g’(y)$.

Composition of Functions

We saw in§1.2.3（P.41）that the inverse $f^{-1}$ of a bijection $f$ is itself a function. Another operation on functions is composition: We can define a new function by composing two functions, $f$ and $g$, i.e., by first applying $f$ and then $g$. Of course, this is only possible if the ranges and domains match, i.e., the range of $f$ must be a subset of the domain of $g$. This operation on functions is the analogue of the operation of relative product on relations from§1.1.6（P.34）.

A diagram might help to explain the idea of composition. In Figure 1.7, we depict two functions $f \colon A \to B$ and $g \colon B \to C$ and their composition $(g\circ f)$. The function $(g\circ f) \colon A \to C$ pairs each element of $A$ with a element of $C$. We specify which element of $C$ a element of $A$ is paired with as follows: given an input $x \in A$, first apply the function $f$ to $x$, which will output some $f(x) = y \in B$, then apply the function $g$ to $y$, which will output some $g(f(x)) = g(y) = z \in C$.

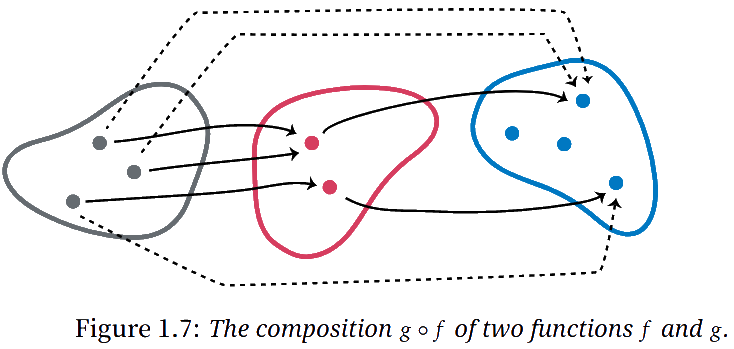
Problem 1.19
Show that if $f \colon A \to B$ and $g \colon B \to C$ are both injective, then $g\circ f\colon A \to C$ is injective.

Problem 1.20
Show that if $f \colon A \to B$ and $g \colon B \to C$ are both surjective, then $g\circ f\colon A \to C$ is surjective.

Problem 1.21
Suppose $f \colon A \to B$ and $g \colon B \to C$. Show that the graph of $g\circ f$ is $R_f \mid R_g$.

Partial Functions

It is sometimes useful to relax the definition of function so that it is not required that the output of the function is defined for all possible inputs. Such mappings are called partial functions.

Problem 1.22
Given $f\colon A \nrightarrow B$, define the partial function $g\colon B \nrightarrow A$ by: for any $y \in B$, if there is a unique $x \in A$ such that $f(x) = y$, then $g(y) = x$; otherwise $g(y) \uparrow$. Show that if $f$ is injective, then $g(f(x)) = x$ for all $x \in \text{dom}(f)$, and $f(g(y)) = y$ for all $y \in \text{ran}(f)$.

命題 1.9 之證明
Suppose there is a $y$ such that $Rxy$. If there were another $y’ \neq y$ such that $Rxy’$, the condition on $R$ would be violated. Hence, if there is a $y$ such that $Rxy$, that $y$ is unique, and so $f$ is well-defined. Obviously, $R_f = R$ and $f$ is total if $R$ is serial.

基数：集合大小的度量

This section discusses enumerations, countability and uncountability. Several sections come in two versions: a more elementary one, that takes enumerations to be lists, or surjections from $\mathbb{Z}^{+}$; and a more abstract onethat defines enumerations as bijections with $\mathbb{N}$.

Introduction

When Georg Cantor developed set theory in the 1870s, one of his aims was to make palatable the idea of an infinite collection—an actual infinity, as the medievals would say. A key part of this was his treatment of the size of different sets. If $a$, $b$ and $c$ are all distinct, then the set $\lbrace a, b, c\rbrace $ is intuitively larger than $\lbrace a, b\rbrace$. But what about infinite sets? Are they all as large as each other? It turns out that they are not.

The first important idea here is that of an enumeration. We can list every finite set by listing all its elements. For some infinite sets, we can also list all their elements if we allow the list itself to be infinite. Such sets are called enumerable. Cantor’s surprising result, which we will fully understand by the end of this section, was that some infinite sets are not enumerable.

Enumerations and enumerable Sets

This section discusses enumerations of sets, defining them as surjections from $\mathbb{Z}^{+}$. It does things slowly, for readers with little mathematical background. An alternative, terser version is given in §1.3.10（P.62）, which defines enumerations differently: as bijections with $\mathbb{N}$ (or an initial segment).

We’ve already given examples of sets by listing their elements. Let’s discuss in more general terms how and when we can list the elements of a set, even if that set is infinite.

A couple of points about enumerations:

1. We count as enumerations only lists which have a beginning and in which every element other than the first has a single element immediately preceding it. In other words, there are only finitely many elements between the first element of the list and any other element. In particular, this means that every element of an enumeration has a finite position: the first element has position $1$, the second position $2$, etc.
2. We can have different enumerations of the same set $A$ which differ by the order in which the elements appear: $4$, $1$, $25$, $16$, $9$ enumerates the (set of the) first five square numbers just as well as $1$, $4$, $9$, $16$, $25$ does.
3. Redundant enumerations are still enumerations: $1$, $1$, $2$, $2$, $3$, $3, \cdots$, enumerates the same set as $1$, $2$, $3, \cdots$, does.
4. Order and redundancy do matter when we specify an enumeration: we can enumerate the positive integers beginning with $1$, $2$, $3$, $1, \cdots$, but the pattern is easier to see when enumerated in the standard way as $1$, $2$, $3$, $4, \cdots$.
5. Enumerations must have a beginning: \cdots, $3$, $2$, $1$ is not an enumeration of the positive integers because it has no first element. To see how this follows from the informal definition, ask yourself, “at what position in the list does the number 76 appear?''
6. The following is not an enumeration of the positive integers: $1$, $3$, $5, \cdots, 2$, $4$, $6, \cdots$. The problem is that the even numbers occur at places $\infty + 1$, $\infty + 2$, $\infty + 3$, rather than at finite positions.
7. The empty set is enumerable: it is enumerated by the empty list!

命題 1.10 之證明
Suppose $A$ has an enumeration $x_1$, $x_2, \cdots$, in which each $x_i$ is an element of $A$. We can remove repetitions from an enumeration by removing repeated elements. For instance, we can turn the enumeration into a new one in which we list $x_i$ if it is an element of $A$ that is not among $x_1, \cdots, x_{i-1}$ or remove $x_i$ from the list if it already appears among $x_1, \cdots, x_{i-1}$.

The last argument shows that in order to get a good handle on enumerations and enumerable sets and to prove things about them, we need a more precise definition. The following provides it.

Let’s convince ourselves that the formal definition and the informal definition using a possibly infinite list are equivalent. First, any surjective function from $\mathbb{Z}^{+}$ to a set $A$ enumerates $A$. Such a function determines an enumeration as defined informally above: the list $f(1)$, $f(2)$, $f(3), \cdots$. Since $f$ is surjective, every element of $A$ is guaranteed to be the value of $f(n)$ for some $n \in \mathbb{Z}^{+}$. Hence, every element of $A$ appears at some finite position in the list. Since the function may not be injective, the list may be redundant, but that is acceptable (as noted above).

On the other hand, given a list that enumerates all elements of $A$, we can define a surjective function $f\colon \mathbb{Z}^{+} \to A$ by letting $f(n)$ be the $n$th element of the list, or the final element of the list if there is no $n$th element. The only case where this does not produce a surjective function is when $A$ is empty, and hence the list is empty. So, every non-empty list determines a surjective function $f\colon \mathbb{Z}^{+} \to A$.

Problem 1.23
Define an enumeration of the positive squares $1$, $4$, $9$, $16, \cdots$

Problem 1.24
Show that if $A$ and $B$ are enumerable, so is $A \cup B$. To do this, suppose there are surjective functions $f\colon \mathbb{Z}^{+} \to A$ and $g\colon \mathbb{Z}^{+} \to B$, and define a surjective function $h\colon \mathbb{Z}^{+} \to A \cup B$ and prove that it is surjective. Also consider the cases where $A$ or $B = \varnothing$.

Problem 1.25
Show that if $B \subseteq A$ and $A$ is enumerable, so is $B$. To do this, suppose there is a surjective function $f\colon \mathbb{Z}^{+} \to A$. Define a surjective function $g\colon \mathbb{Z}^{+} \to B$ and prove that it is surjective. What happens if $B = \varnothing$?

Problem 1.26
Show by induction on $n$ that if $A_1$, $A_2, \cdots, A_n$ are all enumerable, so is $A_1 \cup \cdots \cup A_n$. You may assume the fact that if two sets $A$ and $B$ are enumerable, so is $A \cup B$.

Although it is perhaps more natural when listing the elements of a set to start counting from the $1$st element, mathematicians like to use the natural numbers $\mathbb{N}$ for counting things. They talk about the $0$th, $1$st, $2$nd, and so on, elements of a list. Correspondingly, we can define an enumeration as a surjective function from $\mathbb{N}$ to $A$. Of course, the two definitions are equivalent.

命題 1.11 之證明
Given a surjection $f\colon \mathbb{Z}^{+} \to A$, we can define $g(n) = f(n+1)$ for all $n \in \mathbb{N}$. It is easy to see that $g\colon \mathbb{N} \to A$ is surjective. Conversely, given a surjection $g\colon \mathbb{N} \to A$, define $f(n) = g(n+1)$.

This gives us the following result:

We discussed above than an list of elements of a set $A$ can be turned into a list without repetitions. This is also true for enumerations, but a bit harder to formulate and prove rigorously. Any function $f\colon \mathbb{Z}^{+} \to A$ must be defined for all $n \in \mathbb{Z}^{+}$. If there are only finitely many elements in $A$ then we clearly cannot have a function defined on the infinitely many elements of $\mathbb{Z}^{+}$ that takes as values all the elements of $A$ but never takes the same value twice. In that case, i.e., in the case where the list without repetitions is finite, we must choose a different domain for $f$, one with only finitely many elements. Not having repetitions means that $f$ must be injective. Since it is also surjective, we are looking for a bijection between some finite set $\lbrace 1, \cdots, n\rbrace $ or $\mathbb{Z}^{+}$ and $A$.

命題 1.12 之證明
We define the function $g$ recursively: Let $g(1) = f(1)$. If $g(i)$ has already been defined, let $g(i+1)$ be the first value of $f(1), f(2),\cdots$, not already among $g(1), \cdots, g(i)$, if there is one. If $A$ has just $n$ elements, then $g(1), \cdots, g(n)$ are all defined, and so we have defined a function $g\colon \lbrace 1, \cdots, n\rbrace \to A$. If $A$ has infinitely many elements, then for any $i$ there must be an element of $A$ in the enumeration $f(1)$, $f(2), \cdots$, which is not already among $g(1), \cdots, g(i)$. In this case we have defined a funtion $g\colon \mathbb{Z}^{+} \to A$.
The function $g$ is surjective, since any element of $A$ is among $f(1)$, $f(2)$, \cdots{} (since $f$ is surjective) and so will eventually be a value of $g(i)$ for some $i$. It is also injective, since if there were $j < i$ such that $g(j) = g(i)$, then $g(i)$ would already be among $g(1), \cdots, g(i-1)$, contrary to how we defined $g$.

推論 1.1 之證明
$A$ is enumerable iff $A$ is empty or there is a surjective $f\colon \mathbb{Z}^{+} \to A$. By Proposition 1.12, the latter holds iff there is a bijective function $f\colon Z \to A$ where $Z = \mathbb{Z}^{+}$ or $Z = \lbrace 1, \cdots, n\rbrace $ for some $n \in \mathbb{Z}^{+}$. By the same argument as in the proof of Proposition 1.11, that in turn is the case iff there is a bijection $g\colon N \to A$ where either $N = \mathbb{N}$ or $N = \lbrace 0, \cdots, n-1\rbrace $.

Problem 1.3
According to Definition1.48（P.63）, a set $A$ is enumerable iff $A = \varnothing$ or there is a surjective $f\colon \mathbb{Z}^{+} \to A$. It is also possible to define “enumerable set” precisely by: a set is enumerable iff there is a injective function $g\colon A \to \mathbb{Z}^{+}$. Show that the definitions are equivalent, i.e., show that there is a injective function $g\colon A \to \mathbb{Z}^{+}$ iff either $A = \varnothing$ or there is a surjective $f\colon \mathbb{Z}^{+} \to A$.

Cantor’s Zig-Zag Method

We’ve already considered some “easy’’ enumerations. Now we will consider something a bit harder. Consider the set of pairs of natural numbers, which we defined in§1.0.4（P.22）defined by: $$\mathbb{N} \times \mathbb{N} = \lbrace ⟨n,m⟩: n,m \in \mathbb{N}\rbrace$$ We can organize these ordered pairs into an array, like so:

$$ \begin{array}{ c | c | c | c | c | c} & \mathbf 0 & \mathbf 1 & \mathbf 2 & \mathbf 3 & \cdots \\ \hline \mathbf 0 & ⟨0,0⟩ & ⟨0,1⟩ & ⟨0,2⟩ & ⟨0,3⟩ & \cdots \\ \hline \mathbf 1 & ⟨1,0⟩ & ⟨1,1⟩ & ⟨1,2⟩ & ⟨1,3⟩ & \cdots \\ \hline \mathbf 2 & ⟨2,0⟩ & ⟨2,1⟩ & ⟨2,2⟩ & ⟨2,3⟩ & \cdots \\ \hline \mathbf 3 & ⟨3,0⟩ & ⟨3,1⟩ & ⟨3,2⟩ & ⟨3,3⟩ & \cdots \\ \hline \vdots & \vdots & \vdots & \vdots & \vdots & \ddots\\ \end{array} $$

Clearly, every ordered pair in $\mathbb{N} \times \mathbb{N}$ will appear exactly once in the array. In particular, $⟨n,m⟩$ will appear in the $n$th row and $m$th column. But how do we organize the elements of such an array into a “one-dimensional’’ list? The pattern in the array below demonstrates one way to do this (although of course there are many other options):

$$ \begin{array}{ c | c | c | c | c | c | c} & \mathbf 0 & \mathbf 1 & \mathbf 2 & \mathbf 3 & \mathbf 4 &\cdots \\ \hline \mathbf 0 & 0 & 1& 3 & 6& 10 &\cdots \\ \hline \mathbf 1 &2 & 4& 7 & 11 & \cdots &\cdots \\ \hline \mathbf 2 & 5 & 8 & 12 & \cdots & \cdots&\cdots \\ \hline \mathbf 3 & 9 & 13 & \cdots & \cdots & \cdots & \cdots \\ \hline \mathbf 4 & 14 & \cdots & \cdots & \cdots & \cdots & \cdots \\ \hline \vdots & \vdots & \vdots & \vdots & \vdots&\cdots & \ddots\\ \end{array} $$

This pattern is called Cantor’s zig-zag method. It enumerates $\mathbb{N} \times \mathbb{N}$ as follows: $$⟨0,0⟩, ⟨0,1⟩, ⟨1,0⟩, ⟨0,2⟩, ⟨1,1⟩, ⟨2,0⟩, ⟨0,3⟩, ⟨1,2⟩, ⟨2,1⟩, ⟨3,0⟩, \cdots$$

And this establishes the following:

命題 1.13 之證明
Let $f \colon \mathbb{N} \to \mathbb{N}\times\mathbb{N}$ take each $k \in \mathbb{N}$ to the tuple $⟨n,m⟩ \in \mathbb{N} \times \mathbb{N}$ such that $k$ is the value of the $n$th row and $m$th column in Cantor’s zig-zag array.

This technique also generalises rather nicely. For example, we can use it to enumerate the set of ordered triples of natural numbers, i.e.: $$\mathbb{N} \times \mathbb{N} \times \mathbb{N} = \Setabs{⟨n,m,k⟩}{n,m,k \in \mathbb{N}}$$ We think of $\mathbb{N} \times \mathbb{N} \times \mathbb{N}$ as the Cartesian product of $\mathbb{N} \times \mathbb{N}$ with $\mathbb{N}$, that is, $$\mathbb{N}^3 = (\mathbb{N} \times \mathbb{N}) \times \mathbb{N} =\lbrace ⟨⟨n,m⟩,k⟩: n, m, k
\in \mathbb{N}\rbrace $$ and thus we can enumerate $\mathbb{N}^3$ with an array by labelling one axis with the enumeration of $\mathbb{N}$, and the other axis with the enumeration of $\mathbb{N}^2$:

$$ \begin{array}{ c | c | c | c | c | c} & \mathbf 0 & \mathbf 1 & \mathbf 2 & \mathbf 3 & \cdots \\ \hline \mathbf{⟨0,0⟩} & ⟨0,0,0⟩ & ⟨0,0,1⟩ & ⟨0,0,2⟩ & ⟨0,0,3⟩ & \cdots \\ \hline \mathbf{⟨0,1⟩} & ⟨0,1,0⟩ & ⟨0,1,1⟩ & ⟨0,1,2⟩ & ⟨0,1,3⟩ & \cdots \\ \hline \mathbf{⟨1,0⟩} & ⟨1,0,0⟩ & ⟨1,0,1⟩ & ⟨1,0,2⟩ & ⟨1,0,3⟩ & \cdots \\ \hline \mathbf{⟨0,2⟩} & ⟨0,2,0⟩ & ⟨0,2,1⟩ & ⟨0,2,2⟩ & ⟨0,2,3⟩ & \cdots\\ \hline \vdots & \vdots & \vdots & \vdots & \vdots & \ddots \\ \end{array} $$

Thus, by using a method like Cantor’s zig-zag method, we may similarly obtain an enumeration of $\mathbb{N}^3$. And we can keep going, obtaining enumerations of $\mathbb{N}^n$ for any natural number $n$. So, we have:

Pairing Functions and Codes

Cantor’s zig-zag method makes the enumerability of $\mathbb{N}^n$ visually evident. But let us focus on our array depicting $\mathbb{N}^2$. Following the zig-zag line in the array and counting the places, we can check that $⟨1,2⟩$ is associated with the number $7$. However, it would be nice if we could compute this more directly. That is, it would be nice to have to hand the inverse of the zig-zag enumeration, $g\colon \mathbb{N}^2 \to \mathbb{N}$, such that

\begin{align*} & g(⟨0,0⟩) = 0,\;\\ & g(⟨0,1⟩) = 1,\;\\ & g(⟨1,0⟩) = 2, \; \cdots,\\ & g(⟨1,2⟩) = 7, \; \cdots \end{align*}

This would enable to calculate exactly where $⟨n, m⟩$ will occur in our enumeration.

In fact, we can define $g$ directly by making two observations. First: if the $n$th row and $m$th column contains value $v$, then the $(n+1)$st row and $(m-1)$st column contains value $v + 1$. Second: the first row of our enumeration consists of the triangular numbers, starting with $0$, $1$, $3$, $5$, etc. The $k$th triangular number is the sum of the natural numbers $< k$, which can be computed as $k(k+1)/2$. Putting these two observations together, consider this function: $$g(n,m) = \frac{(n+m+1)(n+m)}{2} + n$$ We often just write $g(n, m)$ rather that $g(⟨n, m⟩)$, since it is easier on the eyes. This tells you first to determine the $(n+m)^\text{th}$ triangle number, and then subtract $n$ from it. And it populates the array in exactly the way we would like. So in particular, the pair $⟨1, 2⟩$ is sent to $\frac{4 \times 3}{2} + 1 = 7$.

This function $g$ is the inverse of an enumeration of a set of pairs. Such functions are called pairing functions.

We can use pairing functions encode, e.g., pairs of natural numbers; or, in other words, we can represent each pair of elements using a single number. Using the inverse of the pairing function, we can decode the number, i.e., find out which pair it represents.

Problem 1.28
Give an enumeration of the set of all non-negative rational numbers.

Problem 1.29
Show that $\mathbb{Q}$ is enumerable. Recall that any rational number can be written as a fraction $z/m$ with $z \in \mathbb{Z}$, $m \in \mathbb{N}^+$.

Problem 1.30
Define an enumeration of $\mathbb{B}^*$.

Problem 1.31
Recall from your introductory logic course that each possible truth table expresses a truth function. In other words, the truth functions are all functions from $\mathbb{B}^k \to \mathbb{B}$ for some $k$. Prove that the set of all truth functions is enumerable.

Problem 1.32
Show that the set of all finite subsets of an arbitrary infinite enumerable set is enumerable.

Problem 1.33
A subset of $\mathbb{N}$ is said to be cofinite iff it is the complement of a finite set $\mathbb{N}$; that is, $A \subseteq \mathbb{N}$ is cofinite iff $\mathbb{N}\setminus A$ is finite. Let $I$ be the set whose elements are exactly the finite and cofinite subsets of $\mathbb{N}$. Show that $I$ is enumerable.

Problem 1.34
Show that the enumerable union of enumerable sets is enumerable. That is, whenever $A_1$, $A_2$, \cdots{} are sets, and each $A_i$ is enumerable, then the union $\bigcup_{i=1}^\infty A_i$ of all of them is also enumerable. [NB: this is hard!]

Problem 1.35
Let $f \colon A \times B \to \mathbb{N}$ be an arbitrary pairing function. Show that the inverse of $f$ is an enumeration of $A \times B$.

Problem 1.36
Specify a function that encodes $\mathbb{N}^3$.

An Alternative Pairing Function

There are other enumerations of $\mathbb{N}^2$ that make it easier to figure out what their inverses are. Here is one. Instead of visualizing the enumeration in an array, start with the list of positive integers associated with (initially) empty spaces. Imagine filling these spaces successively with pairs $⟨n,m⟩$ as follow. Starting with the pairs that have $0$ in the first place (i.e., pairs $⟨0,m⟩$), put the first (i.e., $⟨0,0⟩$) in the first empty place, then skip an empty space, put the second (i.e., $⟨0,2⟩$) in the next empty place, skip one again, and so forth. The (incomplete) beginning of our enumeration now looks like this

$$ \begin{array}{@{}c c c c c c c c c c c@{}} \mathbf 1 & \mathbf 2 & \mathbf 3 & \mathbf 4 & \mathbf 5 & \mathbf 6 & \mathbf 7 & \mathbf 8 & \mathbf 9 & \mathbf{10} & \cdots \\ \\ ⟨0,1⟩ & & ⟨0,2⟩ & & ⟨0,3⟩ & & ⟨0,4⟩ & & ⟨0,5⟩ & & \cdots \\ \end{array} $$

Repeat this with pairs $⟨1,m⟩$ for the place that still remain empty, again skipping every other empty place:

$$ \begin{array}{@{}c c c c c c c c c c c@{}} \mathbf 1 & \mathbf 2 & \mathbf 3 & \mathbf 4 & \mathbf 5 & \mathbf 6 & \mathbf 7 & \mathbf 8 & \mathbf 9 & \mathbf{10} & \cdots \\ \\ ⟨0,0⟩ & ⟨1,0⟩ & ⟨0,1⟩ & & ⟨0,2⟩ & ⟨1,1⟩ & ⟨0,3⟩ & & ⟨0,4⟩ & ⟨1,2⟩ & \cdots \\ \end{array} $$

Enter pairs $⟨2,m⟩$, $⟨2,m⟩$, etc., in the same way. Our completed enumeration thus starts like this:

$$ \begin{array}{@{}cc c c c c c c c c c@{}} \mathbf 1 & \mathbf 2 & \mathbf 3 & \mathbf 4 & \mathbf 5 & \mathbf 6 & \mathbf 7 & \mathbf 8 & \mathbf 9 & \mathbf{10} & \cdots \\ \\ ⟨0,0⟩ & ⟨1,0⟩ & ⟨0,1⟩ & ⟨2,0⟩ & ⟨0,2⟩ & ⟨1,1⟩ & ⟨0,3⟩ & ⟨3,0⟩ & ⟨0,4⟩ & ⟨1,2⟩ & \cdots \\ \end{array} $$

If we number the cells in the array above according to this enumeration, we will not find a neat zig-zag line, but this arrangement:

$$ \begin{array}{ c | c | c | c | c | c | c | c } & \mathbf 0 & \mathbf 1 & \mathbf 2 & \mathbf 3 & \mathbf 4 & \mathbf 5 & \cdots \\ \hline \mathbf 0 & 1 & 3 & 5 & 7 & 9 & 11 & \cdots \\ \hline \mathbf 1 & 2 & 6 & 10 & 14 & 18 & \cdots & \cdots \\ \hline \mathbf 2 & 4 & 12 & 20 & 28 & \cdots & \cdots & \cdots \\ \hline \mathbf 3 & 8 & 24 & 40 & \cdots & \cdots & \cdots & \cdots \\ \hline \mathbf 4 & 16 & 48 & \cdots & \cdots & \cdots & \cdots & \cdots \\ \hline \mathbf 5 & 32 & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ \hline \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \ddots\\ \end{array} $$

We can see that the pairs in row $0$ are in the odd numbered places of our enumeration, i.e., pair $⟨0,m⟩$ is in place $2m+1$; pairs in the second row, $⟨1,m⟩$, are in places whose number is the double of an odd number, specifically, $2 \cdot (2m+1)$; pairs in the third row, $⟨2,m⟩$, are in places whose number is four times an odd number, $4 \cdot (2m+1)$; and so on. The factors of $(2m+1)$ for each row, $1$, $2$, $4$, $8$, \cdots, are exactly the powers of $2$: $1= 2^0$, $2 = 2^1$, $4 = 2^2$, $8 = 2^3, \cdots$.In fact, the relevant exponent is always the first member of the pair in question. Thus, for pair $⟨n,m⟩$ the factor is $2^n$. This gives us the general formula: $2^n \cdot (2m+1)$. However, this is a mapping of pairs to positive integers, i.e., $⟨0,0⟩$ has position $1$. If we want to begin at position $0$ we must subtract $1$ from the result. This gives us:

Accordingly, in our second enumeration of $\mathbb{N}^2$, the pair $⟨0,0⟩$ has code $h(0,0) = 2^0(2\cdot 0+1) - 1 = 0$; $⟨1,2⟩$ has code $2^{1} \cdot (2 \cdot 2 + 1) - 1 = 2 \cdot 5 - 1 = 9$; $⟨2,6⟩$ has code $2^{2} \cdot (2 \cdot 6 + 1) - 1 = 51$.

Sometimes it is enough to encode pairs of natural numbers $\mathbb{N}^2$ without requiring that the encoding is surjective. Such encodings have inverses that are only partial functions.

Nonenumerable Sets

This section proves the non-enumerability of $\mathbb{B}^\omega$ and $\mathscr{P}({\mathbb{Z})^{+}}$ using the definition in§1.3.1（P.45）. It is designed to be a little more elementary and a little more detailed than the version in §1.3.10（P.62）.

Some sets, such as the set $\mathbb{Z}^{+}$ of positive integers, are infinite. So far we’ve seen examples of infinite sets which were all enumerable. However, there are also infinite sets which do not have this property. Such sets are called nonenumerable.

First of all, it is perhaps already surprising that there are nonenumerable sets. For any enumerable set $A$ there is a surjective function $f \colon \mathbb{Z}^{+} \to A$. If a set is nonenumerable there is no such function. That is, no function mapping the infinitely many elements of $\mathbb{Z}^{+}$ to $A$ can exhaust all of $A$. So there are “more’’ elements of $A$ than the infinitely many positive integers.

How would one prove that a set is nonenumerable? You have to show that no such surjective function can exist. Equivalently, you have to show that the elements of $A$ cannot be enumerated in a one way infinite list. The best way to do this is to show that every list of elements of $A$ must leave at least one element out; or that no function $f\colon \mathbb{Z}^{+} \to A$ can be surjective. We can do this using Cantor’s diagonal method. Given a list of elements of $A$, say, $x_1$, $x_2, \cdots$, we construct another element of $A$ which, by its construction, cannot possibly be on that list.

Our first example is the set $\mathbb{B}^\omega$ of all infinite, non-gappy sequences of $0$’s and $1$’s.

Theorem 1.1 之證明
Suppose, by way of contradiction, that $\mathbb{B}^\omega$ is enumerable, i.e., suppose that there is a list $s_{1}$, $s_{2}$, $s_{3}$, $s_{4}, \cdots$, of all elements of $\mathbb{B}^\omega$. Each of these $s_i$ is itself an infinite sequence of $0$’s and $1$’s. Let’s call the $j$-th element of the $i$-th sequence in this list $s_i(j)$. Then the $i$-th sequence $s_i$ is $$s_i(1), s_i(2), s_i(3), \cdots$$

We may arrange this list, and the elements of each sequence $s_i$ in it, in an array:

$$ \begin{array}{c|c|c|c|c|c} & 1 & 2 & 3 & 4 & \cdots \\\hline 1 & \mathbf{s_{1}(1)} & s_{1}(2) & s_{1}(3) & s_1(4) & \cdots \\\hline 2 & s_{2}(1)& \mathbf{s_{2}(2)} & s_2(3) & s_2(4) & \cdots \\\hline 3 & s_{3}(1)& s_{3}(2) & \mathbf{s_3(3)} & s_3(4) & \cdots \\\hline 4 & s_{4}(1)& s_{4}(2) & s_4(3) & \mathbf{s_4(4)} & \cdots \\\hline \vdots & \vdots & \vdots & \vdots & \vdots & \mathbf{\ddots} \end{array} $$

The labels down the side give the number of the sequence in the list $s_1$, $s_2$, \cdots; the numbers across the top label the elements of the individual sequences. For instance, $s_{1}(1)$ is a name for whatever number, a $0$ or a $1$, is the first element in the sequence $s_{1}$, and so on.

Now we construct an infinite sequence, $\overline{s}$, of $0$’s and $1$’s which cannot possibly be on this list. The definition of $\overline{s}$ will depend on the list $s_1$, $s_2, \cdots$. Any infinite list of infinite sequences of $0$’s and $1$’s gives rise to an infinite sequence $\overline{s}$ which is guaranteed to not appear on the list.

To define $\overline{s}$, we specify what all its elements are, i.e., we specify $\overline{s}(n)$ for all $n \in \mathbb{Z}^{+}$. We do this by reading down the diagonal of the array above (hence the name “diagonal method’’) and then changing every $1$ to a $0$ and every $1$ to a $0$. More abstractly, we define $\overline{s}(n)$ to be $0$ or $1$ according to whether the $n$-th element of the diagonal, $s_n(n)$, is $1$ or $0$.

$$ \overline{s}(n) = \begin{cases} 1 & \text{if $s_{n}(n) = 0$}\\ 0 & \text{if $s_{n}(n) = 1$}. \end{cases} $$

If you like formulas better than definitions by cases, you could also define $\overline{s}(n) = 1 - s_n(n)$.

Clearly $\overline{s}$ is an infinite sequence of $0$’s and $1$’s, since it is just the mirror sequence to the sequence of $0$’s and $1$’s that appear on the diagonal of our array. So $\overline{s}$ is an element of $\mathbb{B}^\omega$. But it cannot be on the list $s_1$, $s_2, \cdots$, Why not?

It can’t be the first sequence in the list, $s_1$, because it differs from $s_1$ in the first element. Whatever $s_1(1)$ is, we defined $\overline{s}(1)$ to be the opposite. It can’t be the second sequence in the list, because $\overline{s}$ differs from $s_2$ in the second element: if $s_2(2)$ is $0$, $\overline{s}(2)$ is $1$, and vice versa. And so on.

More precisely: if $\overline{s}$ were on the list, there would be some $k$ so that $\overline{s} = s_{k}$. Two sequences are identical iff they agree at every place, i.e., for any $n$, $\overline{s}(n) = s_{k}(n)$. So in particular, taking $n = k$ as a special case, $\overline{s}(k) = s_{k}(k)$ would have to hold. $s_k(k)$ is either $0$ or $1$. If it is $0$ then $\overline{s}(k)$ must be $1$—that’s how we defined $\overline{s}$. But if $s_k(k) = 1$ then, again because of the way we defined $\overline{s}$, $\overline{s}(k) = 0$. In either case $\overline{s}(k) \neq s_{k}(k)$.

We started by assuming that there is a list of elements of $\mathbb{B}^\omega$, $s_1$, $s_2, \cdots$, From this list we constructed a sequence $\overline{s}$ which we proved cannot be on the list. But it definitely is a sequence of $0$’s and $1$’s if all the $s_i$ are sequences of $0$’s and $1$’s, i.e., $\overline{s} \in \mathbb{B}^\omega$. This shows in particular that there can be no list of all elements of $\mathbb{B}^\omega$, since for any such list we could also construct a sequence $\overline{s}$ guaranteed to not be on the list, so the assumption that there is a list of all sequences in $\mathbb{B}^\omega$ leads to a contradiction. $\blacksquare$

This proof method is called “diagonalization’’ because it uses the diagonal of the array to define $\overline{s}$. Diagonalization need not involve the presence of an array: we can show that sets are not enumerable by using a similar idea even when no array and no actual diagonal is involved.

Theorem 1.2 之證明
We proceed in the same way, by showing that for every list of subsets of $\mathbb{Z}^{+}$ there is a subset of $\mathbb{Z}^{+}$ which cannot be on the list. Suppose the following is a given list of subsets of $\mathbb{Z}^{+}$: $$ Z_{1}, Z_{2}, Z_{3}, \cdots $$ We now define a set $\overline{Z}$ such that for any $n \in \mathbb{Z}^{+}$, $n \in \overline{Z}$ iff $n \notin Z_{n}$: $$ \overline{Z} = \lbrace n \in \mathbb{Z}^{+}: n \notin Z_n\rbrace$$ $\overline{Z}$ is clearly a set of positive integers, since by assumption each $Z_n$ is, and thus $\overline{Z} \in \mathscr{P}({\mathbb{Z})^{+}}$. But $\overline{Z}$ cannot be on the list. To show this, we’ll establish that for each $k \in \mathbb{Z}^{+}$, $\overline{Z} \neq Z_k$.

So let $k \in \mathbb{Z}^{+}$ be arbitrary. We’ve defined $\overline{Z}$ so that for any $n \in \mathbb{Z}^{+}$, $n \in \overline{Z}$ iff $n \notin Z_n$. In particular, taking $n=k$, $k \in \overline{Z}$ iff $k \notin Z_k$. But this shows that $\overline{Z} \neq Z_k$, since $k$ is an element of one but not the other, and so $\overline{Z}$ and $Z_k$ have different elements. Since $k$ was arbitrary, $\overline{Z}$ is not on the list $Z_1$, $Z_2, \cdots$ $blacksquare$

The preceding proof did not mention a diagonal, but you can think of it as involving a diagonal if you picture it this way: Imagine the sets $Z_1$, $Z_2, \cdots$, written in an array, where each element $j \in Z_i$ is listed in the $j$-th column. Say the first four sets on that list are $\lbrace 1,2,3,\cdots\rbrace $, $\lbrace 2, 4, 6, \cdots\rbrace $, $\lbrace 1,2,5\rbrace $, and $\lbrace 3,4,5,\cdots\rbrace $. Then the array would begin with

$$ \begin{array}{r@{}rrrrrrr} Z_1 = \lbrace & \mathbf{1}, & 2, & 3, & 4, & 5, & 6, & \cdots\rbrace \\ Z_2 = \lbrace & & \mathbf{2}, & & 4, & & 6, & \cdots\rbrace \\ Z_3 = \lbrace & 1, & 2, & & & 5\phantom{,} & & \rbrace \\ Z_4 = \lbrace & & & 3, & \mathbf{4}, & 5, & 6, & \cdots\rbrace \\ \vdots & & & & & \ddots \end{array} $$

Then $\overline{Z}$ is the set obtained by going down the diagonal, leaving out any numbers that appear along the diagonal and include those $j$ where the array has a gap in the $j$-th row/column. In the above case, we would leave out $1$ and $2$, include $3$, leave out $4$, etc.

Problem 1.37
Show that $\mathscr{P}({\mathbb{N})}$ is nonenumerable by a diagonal argument.

Problem 1.38
Show that the set of functions $f \colon \mathbb{Z}^{+} \to \mathbb{Z}^{+}$ is nonenumerable by an explicit diagonal argument. That is, show that if $f_1$, $f_2$, \cdots, is a list of functions and each $f_i\colon \mathbb{Z}^{+} \to \mathbb{Z}^{+}$, then there is some $\overline{f}\colon \mathbb{Z}^{+} \to \mathbb{Z}^{+}$ not on this list.

Reduction

This section proves non-enumerability by reduction, matching the results in §1.3.5（P.53）. An alternative, slightly more condensed version matching the results in §1.3.11（P.64）is provided in§1.3.12（P.66）.

We showed $\mathscr{P}({\mathbb{Z})^{+}}$ to be nonenumerable by a diagonalization argument. We already had a proof that $\mathbb{B}^\omega$, the set of all infinite sequences of $0$s and $1$s, is nonenumerable. Here’s another way we can prove that $\mathscr{P}({\mathbb{Z})^{+}}$ is nonenumerable: Show that if $\mathscr{P}({\mathbb{Z})^{+}}$ is enumerable then $\mathbb{B}^\omega$ is also enumerable. Since we know $\mathbb{B}^\omega$ is not enumerable, $\mathscr{P}({\mathbb{Z})^{+}}$ can’t be either. This is called reducing one problem to another—in this case, we reduce the problem of enumerating $\mathbb{B}^\omega$ to the problem of enumerating $\mathscr{P}({\mathbb{Z})^{+}}$. A solution to the latter—an enumeration of $\mathscr{P}({\mathbb{Z})^{+}}$—would yield a solution to the former—an enumeration of $\mathbb{B}^\omega$.

How do we reduce the problem of enumerating a set $B$ to that of enumerating a set $A$? We provide a way of turning an enumeration of $A$ into an enumeration of $B$. The easiest way to do that is to define a surjective function $f\colon A \to B$. If $x_1$, $x_2, \cdots$, enumerates $A$, then $f(x_1)$, $f(x_2), \cdots$, would enumerate $B$. In our case, we are looking for a surjective function $f\colon \mathscr{P}({\mathbb{Z})^{+}} \to \mathbb{B}^\omega$.

Problem 1.3
Show that if there is an injective function $g\colon B \to A$, and $B$ is nonenumerable, then so is $A$. Do this by showing how you can use $g$ to turn an enumeration of $A$ into one of $B$.

Proof of Theorem 1.6（P.65）by reduction
Suppose that $\mathscr{P}({\mathbb{Z})^{+}}$ were enumerable, and thus that there is an enumeration of it, $Z_{1}$, $Z_{2}$, $Z_{3}, \cdots$

Define the function $f \colon \mathscr{P}({\mathbb{Z})^{+}} \to \mathbb{B}^\omega$ by letting $f(Z)$ be the sequence $s_{k}$ such that $s_{k}(n) = 1$ iff $n \in Z$, and $s_k(n) = 0$ otherwise. This clearly defines a function, since whenever $Z \subseteq \mathbb{Z}^{+}$, any $n \in \mathbb{Z}^{+}$ either is an element of $Z$ or isn’t. For instance, the set $2\mathbb{Z}^{+} = \lbrace 2, 4, 6, \cdots\rbrace $ of positive even numbers gets mapped to the sequence $010101\cdots$, the empty set gets mapped to $0000\cdots$ and the set $\mathbb{Z}^{+}$ itself to $1111\cdots$.

It also is surjective: Every sequence of $0$s and $1$s corresponds to some set of positive integers, namely the one which has as its members those integers corresponding to the places where the sequence has $1$s. More precisely, suppose $s \in \mathbb{B}^\omega$. Define $Z \subseteq \mathbb{Z}^{+}$ by: $$Z = \lbrace n \in \mathbb{Z}^{+}: s(n) = 1\rbrace$$ Then $f(Z) = s$, as can be verified by consulting the definition of $f$.

Now consider the list $$f(Z_1), f(Z_2), f(Z_3), \cdots$$ Since $f$ is surjective, every member of $\mathbb{B}^\omega$ must appear as a value of $f$ for some argument, and so must appear on the list. This list must therefore enumerate all of $\mathbb{B}^\omega$.

So if $\mathscr{P}({\mathbb{Z})^{+}}$ were enumerable, $\mathbb{B}^\omega$ would be enumerable. But $\mathbb{B}^\omega$ is nonenumerable (Theorem 1.5（P.64）). Hence $\mathscr{P}({\mathbb{Z})^{+}}$ is nonenumerable. $\blacksquare$

It is easy to be confused about the direction the reduction goes in. For instance, a surjective function $g \colon \mathbb{B}^\omega \to B$ does not establish that $B$ is nonenumerable. (Consider $g \colon \mathbb{B}^\omega \to \mathbb{B}$ defined by $g(s) = s(1)$, the function that maps a sequence of $0$’s and $1$’s to its first element. It is surjective, because some sequences start with $0$ and some start with $1$. But $\mathbb{B}$ is finite.) Note also that the function $f$ must be surjective, or otherwise the argument does not go through: $f(x_1)$, $f(x_2), \cdots$, would then not be guaranteed to include all the elements of $B$. For instance, $$ h(n) = \underbrace{000\cdots0}_{\text{$n$ $0$’s}} $$ defines a function $h\colon \mathbb{Z}^{+} \to \mathbb{B}^\omega$, but $\mathbb{Z}^{+}$ is enumerable.

Problem 1.40
Show that the set of all sets of pairs of positive integers is nonenumerable by a reduction argument.

Problem 1.41
Show that $\mathbb{N}^\omega$, the set of infinite sequences of natural numbers, is nonenumerable by a reduction argument.

Problem 1.42
Let $P$ be the set of functions from the set of positive integers to the set $\lbrace 0\rbrace $, and let $Q$ be the set of partial functions from the set of positive integers to the set $\lbrace 0\rbrace $. Show that $P$ is enumerable and $Q$ is not. (Hint: reduce the problem of enumerating $\mathbb{B}^\omega$ to enumerating $Q$).

Problem 1.43
Let $S$ be the set of all surjective functions from the set of positive integers to the set $\lbrace 0,1\rbrace$, i.e., $S$ consists of all surjective $f\colon \mathbb{Z}^{+} \to \mathbb{B}$. Show that $S$ is nonenumerable.

Problem 1.44
Show that the set $\mathbb{R}$ of all real numbers is nonenumerable.

The article was recently updated on Saturday, March 18, 2023, 14:28:42 by 王小花.