命題邏輯（propositional logic），也稱語句邏輯（sentential logic），是從聯結詞和複合句的角度討論邏輯蘊涵、可演繹性和一致性。這意味着我們會忽略很多常見的東西，如主詞、謂詞和量詞等。命題和語句其實還是有區別的，但我們在這門課裏暫時不加區分（技術用語除外）。用「命題」方便時用「命題」，用「語句」或「句子」方便時用「語句」或「句子」。

論說的前提和結論都由陳述句（declarative sentence）構成，我們的信念也由陳述句表達。那麼，什麼是陳述句呢？直觀上我們似乎都知道陳述句是什麼樣的句子，但要對這個問題提供一個嚴格而準確的答案是不容易的。目前，我們可以滿足於一個簡單化的答案：對於任何一個語句 $\varphi$，如果我們問「$\varphi$ 是眞的嗎？$\varphi$ 是假的嗎？」是有意義的，那麼我們就稱 $\varphi$ 爲陳述句。［Hodges,1977］針對本書討論的句子，我們有兩個預設：

1. 我們討論的句子只限於陳述句。
2. 我們討論的陳述句只限於非眞即假的陳述句。

如果一個句子是眞的，我們也說該句子的眞值是眞；如果一個句子是假的，我們也說該句子的眞值是假。眞和假統稱爲眞值（truth-values）。用這個概念來重複上面的第一個預設，那就是：我們討論的語句都有眞值；用它來重複上面第二個預設，那就是：我們討論的眞值只有兩個。

學過「邏輯導論」的讀者，對本章大部分內容是熟悉的，這裏權當複習一次。不過，我們並不假設讀者學過「邏輯導論」。本章的內容是自足的，無須預設任何大學課程。當然，沒學過「邏輯導論」的讀者，可能要比學過「邏輯導論」的讀者多花些時間或氣力。

聯結詞與複合句

聯結詞

命題聯結詞（propositional connectives），也作語句聯結詞（sentential connectives），又稱命題算子（propositional operators）或語句算子（sentential operators）。直觀地說，它們是帶空格（序列）的表達式，使得以陳述句填入這些空格的結果總是陳述句。通常，我們將命題聯結詞簡稱爲聯結詞。

對每個自然數 $n > 0$，如果一個聯結詞有 $n$ 個空格，通常就稱它是 $n$ 元聯結詞。習慣上，當說到聯結詞時，人們更喜歡只提聯結詞表達式中的文字（或符號）而省略那些空格。比如，人們會說「並且」是聯結詞，意思是說「$\underline{\hspace{2em}}$並且$\underline{\hspace{2em}}$」是聯結詞；人們也會說「如果–那麼」是二元聯結詞，意思是說「如果$\underline{\hspace{2em}}$那麼$\underline{\hspace{2em}}$」是二元聯結詞。

有些讀者可能會認爲，對聯結詞的上述簡單說法有點怪。比如，

是帶空格的表達式，並且以陳述句填入空格的結果總是陳述句。所以按上述說法，它應該是個一元聯結詞。可是，說這樣的表達式是聯結詞，總覺得有點怪。讀者可以用例 2.0 中的聯結詞造出很複雜的複合句，然後還原若干個空格，從而得到很多與例 2.1 第〇條類似的例子；讀者也可以找到例 2.0 中沒有的符合關於聯結詞的上述説法的「怪」例子，如例 2.1 第一條。

如果覺得例 2.1 的例子怪，大概是因爲它們都包含陳述句而我們稱它們爲聯結詞，但詞中又似乎不該有句。當然，常用的和我們將仔細討論的聯結詞都是（或都對應於）自然語言中的詞或詞組，而且「聯結詞」看上去也應是指有聯結功能的詞或詞組。但是，常用聯結詞是詞或詞組這個事實，不應限制我們對聯結詞的一般情況的討論，而且我們也可以給聯結詞取其他名稱，比如「聯結算子」等（「聯結詞」的使用只是沿襲慣例）。

其實，我們討論的聯結詞不過是陳述句集合上的某種函數（運算）：對每個這樣的 $n$ 元函數，一旦給定有序的 $n$ 個陳述句作爲其自變量的取值，該函數的值是個唯一的陳述句，亦即由給定陳述句依次填入聯結詞的空格序列所得到的句子。

說到函數，讀者一定熟悉自然數集合上的加法運算 +。我們知道它是二元函數：任給兩個自然數 $k$ 和 $n$，一定有唯一的自然數，它是 $k$ 與 $n$ 和，即 $k+n$。如果我們把 $k$ 固定，比如說令 $k=3$，那麼 $3+n$ 還是不是自然數集合上的運算呢？當然還是。

再來看例 2.1 聯結詞的「怪」例子，它們很像 $3+n$ 這樣的函數：將二元聯結詞「如果–那麼」的第一個元的值固定爲「張三和李四是同學」，其結果就是陳述句集合上的一元函數；同理，將二元聯結詞「相信$\underline{\hspace{2em}}$的人認爲$\underline{\hspace{2em}}$。」中的第一個元的值固定爲「太陽繞着地球轉」，其結果也是陳述句集合上的一元函數。

複合句和簡單句

直觀地說，複合句（compound sentence）是其中用到聯結詞的陳述句。不是複合句的陳述句叫做簡單句（simple sentence）。

讀者應注意用（use）與提（mention）的區別。用了聯結詞的語句是複合句，僅僅提到而沒用到聯結詞的語句不是複合句。這也就是爲什麼我們沒有說複合句是包含聯結詞或有聯結詞出現的陳述句，而說複合句是其中用到聯結詞的陳述句。比如

☯例 2.2 張三喜歡用『但是』，但是從來不在該用的地方用。

這句話第二個「但是」是被用作聯結詞的，第一個「但是」只是被提到，沒有被用作聯結詞。所以，「張三喜歡用『但是』」不是複合句——雖然其中有聯結詞「但是」，但它只是被提到而沒有被用到。「用」和「提」的區別是語言哲學中討論的問題。很多人習慣用引號表示「提」，但這種方法也不是完全沒有缺陷的。我們這裏大體上遵循這個習慣。當然，可以被提的不限於聯結詞。

說得具體一些，複合句是用聯結詞聯結某些句子而形成的句子。由此可知，複合句中的某些部分本身也會是陳述句。例如：

作爲複合句的部分而出現的陳述句，既可以是簡單句，也可以是複合句。下面幾個句子中的每一個，都是其後的複合句的部分，但只有第一個纔是簡單句：

複合句的子句

上面討論複合句的部分時，我們雖然還沒有用「子句」和「眞子句」這些詞，但已經涉及相應的概念了。既然複合句是用聯結詞聯結某些句子而形成的句子，那麼簡單地說，那些被聯結的句子就是它的眞子句；相反，簡單句不是用聯結詞聯結某些句子而形成的，從而簡單句沒有眞子句。

一個句子 $\varphi$ 的子句既是 $\varphi$ 的一部分又是完整的句子，但既是 $\varphi$ 的部分又是完整句子的表達式卻未必是 $\varphi$ 的子句。比如複合句

☯例 2.5 張三想起李四的表哥是王五。

它的子句「李四的表哥是王五」既是例 2.5 的部分又是完整的句子。然而，表達式「張三想起李四」同樣既是例 2.5 的部分又是完整的句子，但它不是例 2.5 的子句。例 2.5 是由聯結詞「張三想起」聯結句子「李四的表哥是王五」而形成的，「張三想起李四」並不是用來合成例 2.5 的句子，所以它不應該是例 2.5 的子句。

其實，即使簡單句中也可以有某個眞部分，它本身能組成一個完整的句子。如簡單句

☯例 2.6 張三在學校裏學習很用功。

表達式「張三在學校裏學習」既是例 2.6 的部分又是個完整的句子。顯然，簡單句的部分不能是它的眞子句。假如說例 2.6 有子句「張三在學校裏學習」，那就像是說「邏輯」這個詞中包含了「四」「維」「車」「口」「耳」這些詞。

一個詞當然可以包含另一個詞，組成「合成詞」。如「邏輯課程」這個詞包含了「邏輯」和「課程」兩個詞。通常我們可以說「邏輯」的筆劃中包含了「四」「維」「車」「口」「耳」這些字的筆劃，但這不同於說「邏輯」這個詞包含了「四」「維」「車」「口」「耳」這些詞。如同「category」這個詞，它並沒有包含「cat」「a」「at」「ate」等詞，儘管拼法（spelling）中有這些字母組合。

通常人們說，複合句是「包含其他句子的句子」，簡單句是「不包含其他句子的句子」。從以上討論可知，這只是大概的說法。易見，按這種說法，「張三在學校裏學習」也不是簡單句，因爲它包含了「張三在學校」這樣的句子。有些敎科書的確把複合句定義爲「包含其他句子的句子」，把簡單句定義爲「不包含其他句子的句子」，同樣也只是大概的說法，不能太當眞。自然，假如對「包含」做出足夠的限制，關於複合句和簡單句的這種說法也許能說通。不過那些書中並沒有這種限制。

那麼，應該如何把握複合句的子句和眞子句呢？設 $\varphi$ 和 $\psi$ 都是完整的句子。$\psi$ 是 $\varphi$ 的眞子句（proper subsentence），如果以空格替換 $\varphi$ 中的 $\psi$，其結果是一個聯結詞；$\psi$ 是 $\varphi$ 的子句（subsentence），如果 $\psi$ 是 $\varphi$ 的眞子句或者 $\psi=\varphi$. 直觀地，說 $\psi$ 是 $\varphi$ 的眞子句，是說 $\psi$ 是 $\varphi$ 的一個（眞）部分，並且如果將 $\varphi$ 中的這一部分換成任何其他句子，其結果都還是完整的句子。

根據這個說明，「張三想起李四」不是例 2.5 的眞子句。因爲「張三和李四是好朋友」是句子，用它替換例 2.5 中的「張三想起李四」，其結果是「張三和李四是好朋友的表哥是王五」，這結果顯然不是一個句子。顯然，「張三想起李四」也不是例 2.5 的子句。

類似地，將「張三和李四是好朋友」替換例 2.6 中的「張三在學校裏學習」，其結果是「張三和李四是好朋友很用功」，這個結果也不是句子。所以「張三在學校裏學習」不是例 2.6 的（眞）子句。

複合句的（眞）子句當然是它的（眞）部分。如果覺得眞子句從「部分」的角度容易理解，那麼請記住：它是該複合句的一部分，並在句中被某聯結詞聯結。

主聯結詞和直接子句

主聯結詞

藉助直觀，我們可以明白什麼是一個聯結詞在某複合句中的一個出現。簡單地說，它是指該聯結詞及其在句中所處的一個位置。這個概念顯然可以精確化。比如，我們可以用自然數表示句子中的位置。餘下的就簡單了。一個聯結詞在同一複合句中可以出現多次。下面例句中都有同一聯結詞多次岀現的情況：

☯例 2.7 聯結詞的出現
李四知道有理數和自然數一樣多，然而他不知道實數比有理數多。

☯例 2.8 聯結詞的出現
如果張三聽說過無窮集是分大小的，那麼他大概也聽說過實數比有理數多；但是如果他沒聽說過無窮集有可數無窮集和不可數無窮集，那麼他很可能認爲無窮是不可比的。

一個聯結詞被稱爲一個複合句的主聯結詞（major connective, main operator），如果它在該句中的某個出現不是在該句子的任何眞子句中，並且它不是由多元聯結詞經用句子（或聯結詞）填入其空格得到的聯結詞。如果我們把一個複合句看作是由簡單句經聯結詞一步步構造起來的，那麼，在構造過程的最後一步，我們使用的聯結詞就是這個複合句的主聯結詞。比如「李四知道有理數和自然數一樣多」「李四不知道實數比有理數多」是例 2.7 複合句的真子句，並且例 2.7 的其他真子句都出現在這兩個句中；然而，例 2.7 中的「然而」（唯一一次出現）卻沒有出現在這些句子中。所以，「然而」是例 2.7 的主聯結詞。類似地，「但是」是例 2.8 的主聯結詞。

☯例 2.9 聯結詞的出現
王五相信，如果老師能給出足夠的理由說明實數比有理數多，他也會相信實數比有理數多。

☯例 2.10 聯結詞的出現
如果實數比自然數多，那麼，如果有理數又和自然數一樣多，則實數就比有理數多。

例 2.9 中「王五相信」的第一個出現決定了它是該句的主聯結詞，而第二個出現（「他相信」）與它是主聯結詞無關。類似地，例 2.10 中「如果」的第一個出現決定了它是該句的主聯結詞，而其第二個出現與它是主聯結詞無關。

不難看出，對每一個（沒有歧義的）複合句，都有唯一的聯結詞，它在該句中的某個出現使得它成爲該句的主聯結詞。一個句子中的主聯結詞決定了該句子的基本（命題）結構或基本（命題）形式。

直接子句

不僅同一個聯結詞在一個複合句中可以出現多次，同一個句子也可以作爲子句在一個複合句中出現多次。易見，我們可以精確地刻畫任何表達式（聯結詞、子句、詞和字等）在一複合句中的出現。

☯例 2.11 直接子句
實數比有理數多，但是張三不相信實數比有理數多。

設 $\psi$ 爲 $\varphi$ 的眞子句。 $\psi$ 被稱爲 $\varphi$ 的一個直接子句（direct subsentence），如果 $\psi$ 在 $\varphi$ 中的某個出現不是在 $\varphi$ 的任何其他眞子句中的出現。簡單地說，$\varphi$ 的直接子句就是 $\varphi$ 的主聯結詞聯結的那些子句。像例 2.11 中的「實數比有理數多」，它是例句的眞子句，而且它的第一個（左側的）出現不在例句的任何其他眞子句中，所以它是例 2.11 的一個直接子句。類似地，「張三不相信實數比有理數多」也是例 2.11 的一個直接子句。注意：「實數比有理數多」之所以是例句的直接子句，是因爲它的第一個出現；它的第二個出現（右側的）是在例句的眞子句「張三不相信實數比有理數多」中的出現，與它是例句的直接子句無關。

自然，如果一個複合句的直接子句本身也是複合句，它也會有自己的主聯結詞和自己的直接子句。

☯例 2.12 直接子句
李四相信實數比有理數多，但是張三不相信實數比有理數多。

「李四相信實數比有理數多」「張三不相信實數比有理數多」都是例 2.12 的直接子句，而「實數比有理數多」不再是例 2.12 的直接子句。顯然，例 2.12 的上述直接子句都是複合句，它們又都有自己的直接子句：「實數比有理數多」是「李四相信實數比有理數多」的直接子句，而「張三相信實數比有理數多」是「張三不相信實數比有理數多」的直接子句。

複合句的主聯結詞和直接子句密切相關。一個複合句的主聯結詞，雖然可能在該複合句中出現多次，但使它成爲該句主聯結詞的那個出現，一定聯結了該句的全部直接子句。

眞值、非眞值函數聯結詞

眞值函數聯結詞

對任意的聯結詞，如果以它爲主聯結詞的複合句的眞值完全由該句的直接子句的眞值來決定，那麼這個聯結詞就是眞值函數聯結詞（truth-functional connective）。

非眞值函數聯結詞

如果一個聯結詞不是眞值函數聯結詞，它就是一個非眞值函數聯結詞（non-truth-functional connective）；換言之，如果以它爲主聯結詞的複合句的眞值不能完全由該複合句的直接子句的眞值來決定，那麼它就是一個非眞值函數聯結詞。

要說明一個聯結詞不是眞值函數聯結詞，可以去構造以它爲主聯結詞且滿足下列條件的兩個複合句：

1. 這兩個複合句的眞值不同；
2. 這兩個複合句中對應的直接子句的眞值相同。

☯例 2.15 「張三相信」不是眞值函數聯結詞

1. 張三相信地球圍繞着太陽轉。
2. 張三相信 $2+2=4$。

假定張三生活在天文學極不普及而簡單的加減法已普及的年代或地區。那麼，他會相信 $2+2=4$ 而不相信地球圍繞着太陽轉，也就是說，上述兩個複合句一眞一假。但是，這兩個複合句中對應的直接子句（「地球圍繞着太陽轉」和「$2+2=4$」）卻具有相同的眞值（都是眞的）。

爲什麼這樣做就可以說明給定的聯結詞不是眞值函數聯結詞？要說明給定的聯結詞不是眞值函數聯結詞，只需要說明它不滿足眞值函數聯結詞的定義。在例 2.15 中，兩個複合句中對應的直接子句（「地球圍繞着太陽轉」和「$2+2=4$」）眞值相同，但經「張三相信」聯結而分別形成的兩個複合句卻有不同的眞值。這說明兩個複合句的直接子句的眞值不能完全決定複合句的眞值，那麼根據眞值函數聯結詞的定義，聯結直接子句而構成複合句的主聯結詞「張三相信」就不是眞值函數聯結詞。

☯例 2.16 「自從$\underline{\hspace{2em}}$，$\underline{\hspace{2em}}$」不是眞值函數聯結詞

1. 自從愛因斯坦提出相對論，科學家對宇宙的看法較牛頓時期有很大變化。
2. 自從劉邦打敗了項羽，很多中國人喜歡看足球。

憑藉直觀，我們會認爲例 2.16 第一個句子是眞的，而第二個句子是假的；但是這兩個複合句的所有直接子句都是眞的。這就是說，以「自從」爲主聯結詞的複合句的眞值不能完全由其直接子句的眞值決定。所以，「自從」不是眞值函數聯結詞。

從現在起，除非有特別說明，我們討論的聯結詞將只限於眞值函數聯結詞。

常用的眞值函數聯結詞符號

參見表 2.0，我們用下述符號表示本課程討論的眞值函數聯結詞：

1. $\neg$：否定，並非$\underline{\hspace{2em}}$
2. $\wedge$：合取 ，並且$\underline{\hspace{2em}}$
3. $\vee$：析取， $\underline{\hspace{2em}}$或者$\underline{\hspace{2em}}$
4. $\rightarrow$：蘊涵 ，如果$\underline{\hspace{2em}}$那麼$\underline{\hspace{2em}}$
5. $\leftrightarrow$：等值 ， $\underline{\hspace{2em}}$當且僅當$\underline{\hspace{2em}}$

稱 $\neg$ 爲否定號，稱主聯結詞爲 $\neg$ 的複合句爲否定句；其餘類推。

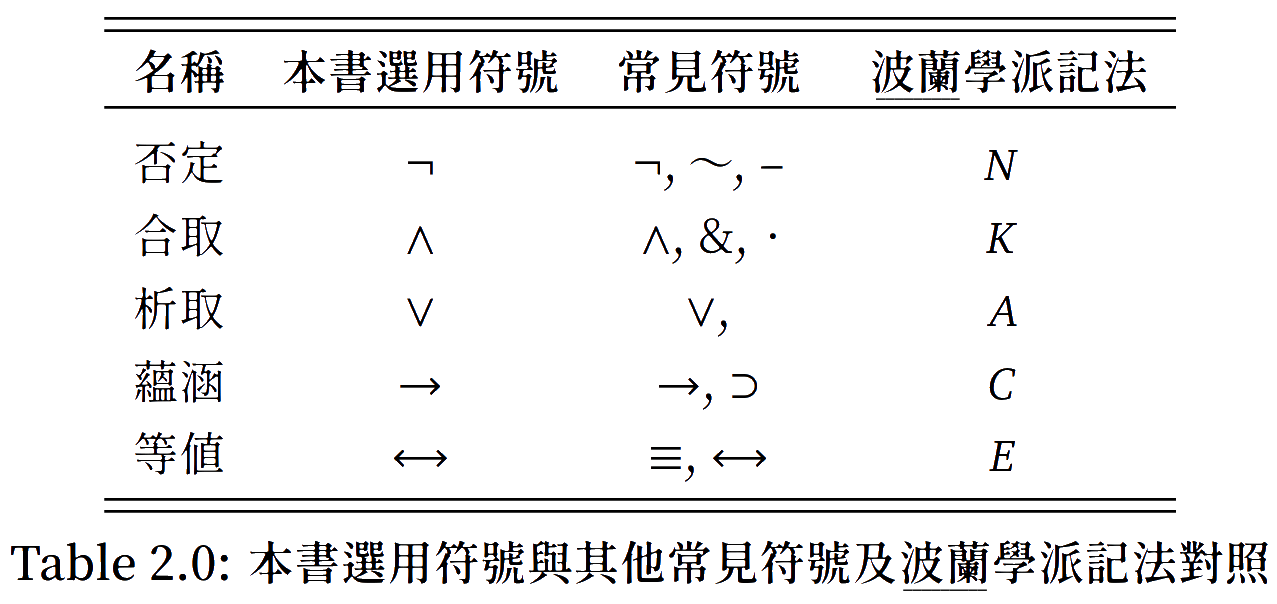
文科學生可能不太熟悉「當且僅當」這個詞，它相當於「等價於」。「$\varphi$ 當且僅當 $\psi$ 」的意思是：如果 $\varphi$ 那麼 $\psi$ 並且如果 $\psi$ 那麼 $\varphi$。「$\varphi$ if and only if $\psi$」的意思就是：$\varphi$ if $\psi$，and $\varphi$ only if $\psi$（其中「$\varphi$ only if $\psi$」和「if $\varphi$ then $\psi$」意思相同）。

符號化

無論讀者是否對命題邏輯層次的符號化（symbolization）已有了解，這種符號化畢竟是相當簡單的，所以我們只簡略地說說。

聯結詞對應符號

學習符號化的目的之一，就是要通過分析自然語言的句子，把握這些句子的邏輯結構。在這一學習過程中，學生需要通過自己的練習，逐步弄清哪些聯結詞與哪些聯結詞的意義相當或相近。下面這個列表當然是不完全的。其實，完全的列表也不是必要的。

1. $\neg$ ：並非，並不，不，……
2. $\wedge$ ： 並且，但是，可是，然而，且，而，卻，不是–而是，……
3. $\vee$：或，或者，或者–或者，要麼–要麼，不是–就是，（除非），……
4. $\rightarrow$：如果，如果–那麼，若–則，只要，一旦，（否則，除非），……
5. $\leftrightarrow$：當且僅當，（等價於），……

符號化的基本操作過程

相對於眞值函數聯結詞簡單的句子，是指那些沒有主聯結詞或沒有使用眞值函數聯結詞做主聯結詞的句子，包括簡單句、以非眞值函數聯結詞爲主聯結詞的句子以及由（隱蔽的）量詞決定了其基本結構的句子等等。（量詞將在謂詞邏輯章節中討論。關於相對於眞值函數聯結詞簡單的句子，上述說明只是一種直觀的說法，並不是定義。）由於我們現在不討論非眞值函數聯結詞和量詞等的符號化，遇到有這種結構的句子就只能和簡單句一樣處理。從現在起，除非有特別說明，簡單句都指相對於眞值函數聯結詞簡單的句子。

以下是命題邏輯符號化的基本步驟：

1. 確認所有簡單的句子及其否定。
2. 如果需要，對句子進行複述，即在不改變句子意思的前提下對句子表面結構做小的改動。
3. 用小寫的英文字母代換簡單句，或者用給出的「辭典」中的字母來代換它們。（用不同的字母代換不同的簡單句。如果有同一個簡單句的多次出現，確保用相同字母代換相同簡單句的所有出現。）
4. 確認所有的聯結詞，並「由內至外」或「由外至內」逐步把句子符號化。

這裏用「辭典」這個詞只是爲了方便。這裏的辭典解釋的不是詞，而是一個個命題變號。倘若用「原子句典」倒是可以避免誤會，但這個詞太怪了，只好還是用「辭典」。

☯例 2.17
如果張三或李四惹怒了王五，那麼，趙六不會替王五打抱不平而洪七會高興地大喫大喝。

解剖層次嵌套，例 2.17 的「辭典」或「原子句典（集）」爲：

1. $p$：張三惹怒了王五。
2. $q$：李四惹怒了王五。
3. $r$：趙六會替王五打抱不平。
4. $s$：洪七會高興地大喫大喝。

☯例 2.18.1 例 2.17 由內至外符號化

1. 如果 $p$ 或者 $q$，那麼，$\neg r$ 而 $s$.
2. 如果 $(p \lor q)$，那麼 $(\neg r \land s)$.
3. $(p \lor q) \rightarrow (\neg r \land s)$.

☯例 2.18.2 例 2.17 由外至內符號化

1. 如果 $p$ 或者 $q$，那麼，$\neg r$ 而 $s$.
2. （$p$ 或者 $q$），$\rightarrow$（$\neg r$ 而 $s$）.
3. $(p \lor q) \rightarrow (\neg r \land s)$

自然語言由於種種因素在表達上不很「規範」，有些表達式（詞的組合）單獨拿出來不是句子，但可以被複述成句子。比如例 2.2 中有「從來不在該用的地方用」這一表達式。如果把它從例 2.2 中抽岀來看，並不能説它是完整的句子；但我們知道，它可以被複述成「張三從來不在該用『但是』的地方用『但是』。」例 2.2 經這樣複述後可以表達爲：

張三喜歡用「但是」，但是張三從來
不在該用「但是」的地方用「但是」。

雖然略顯繁瑣，但只是修辭問題而不是語法問題，還能忍受。

幾種特殊情況

有些複合句的字面結構甚至更難處理。如

☯例 2.19 張三只有加倍努力學習，纔能通過下次考試。

句中的「只有$\underline{\hspace{2em}}$纔（有）$\underline{\hspace{2em}}$」表達了某種條件句的結構，應該是個聯結詞。（「只有–纔」在很多情況下是量詞，這將在§13.6（P.234）中討論。）如果我們在「只有$\underline{\hspace{2em}}$纔（有）$\underline{\hspace{2em}}$」的空格中填入陳述句，得到的結果有時很怪，比如：「只有張三加倍努力，纔有張三能通過下次考試」。這就需要分析句子的各部分及其關係，甚至需要用文字上與原句相差較大的複述來顯示句子的結構。像例 2.19 是說「張三加倍努力學習」是「張三能通過下次考試」的必要條件，所以它可以複述成「如果張三不加倍努力學習，他就不能通過下次考試」。當然，也可以複述成「如果張三能通過下次考試，那麼他加倍努力學習了」。

「只有 $p$ 纔（有）$q$」的符號化結果是「$\neg p \rightarrow \neg q$」或「$q \rightarrow p$」。

「只有–纔」作聯結詞時很像英文的 “only if”. “$p$ only if $q$, “only if $q$, $p$” 和 “if $p$ then $q$” 意思相同。

另一個常見而又有點特殊的聯結詞是「除非」。比如

☯例 2.20 李四下午不會去聽講座，除非他學過數理邏輯。
例 2.20 可以複述成：

1. 如果李四沒有學過數理邏輯，他下午不會去聽講座。（$\neg q \rightarrow \neg p;~~ p \rightarrow q$ ）
2. 或者李四下午不會去聽講座，或者他學過數理邏輯。（$\neg p \lor q$ ）

所以，「除非」的符號化可以和「或者」一樣，也可以和「如果不」一樣。這就是說，

「$p$ 除非 $q$」的符號化結果是「$p \lor q$」或「$\neg q \rightarrow p$」。

例 2.20 本質與「今天要軍訓，除非今天下雨」的結構相同，但它是「$\neg p$ 除非 $q$」的結構。所以，不應死記「$p$ 除非 $q$」的符號化結果，而應理解並掌握「$\underline{\hspace{1.5em}}$除非$\underline{\hspace{1.5em}}$」這種句子結構的複述方式。「除非」大致與英文中的聯結詞「unless」相仿。

論說的符號化

因爲論說由句子組成，所以，只要明白如何將論說中各個句子符號化，那麼整個論說的符號化應是水到渠成的事。不過，有一點要注意：對同一個論說中所有句子的符號化，都必須根據同一個「辭典」來進行。

☯例 2.21 將下列論說符號化

1. 如果蓷蒂是企鵝，那麼蓷蒂是鳥。$\hspace{2em}$ $p \rightarrow q$
2. 蓷蒂不是鳥。$\hspace{2em}$ $\neg q$
3. $\therefore$ 蓷蒂不是企鵝。$\hspace{2em}$ $\therefore \neg p$

形式

我們說過一個論說的好壞在於它的形式的好壞，但對論說的形式是什麼卻說的很少。事實上，要想確切地說出論說的形式甚至命題的形式是什麼，並不是一件容易的事。這裏我們可以說一點點。

在我們把一個論說符號化之後，雖然使用的符號在符號化過程中被賦予了意義，但我們很容易賦予它們別的意義（聯結詞和 “$\therefore$” 除外），甚至很自然地把例 2.21 的符號化結果讀作「如果 $p$ 那麼 $q$,…」，而不讀作「如果蓷蒂是企鵝那麼蓷蒂是鳥，……」。這就是說，我們可以把例 2.21 中的 $p$ 和 $q$ 看作能取不同句子爲值的變元，而當我們這樣做時，我們就是把例 2.21 右列看作例 2.21 左列的形式。通常，人們把一個論說的符號化結果稱作該論說的形式（form），而事實上符號化也常被稱作形式化（formalization）。

在把命題或論說的符號化結果看作它們的形式時，我們要注意幾點：

1. 雖然此時 $p$ 和 $q$ 等符號是可以取任意句子爲值的變元，但 $\neg$, $\land$, $\lor$, $\rightarrow$, $\leftrightarrow$ 卻不是變元，他們固定地表示否定、合取、析取等聯結詞。
2. 這裏說的形式，不是根據自然語言句子中的字的排列，直接用符號替換組成句子和聯結詞的「字段」而得到的。這裏又有兩層意思：

• 句子的形式不是通過機械的「字段/符號」替換就能得到的。（符號化過程中時常要做的複述已經說明了這一點。）
• 符號化依賴於某種邏輯分析的理論。

上述第二層意思需要一點解釋。我們現在使用的邏輯分析理論是非常簡單的，它只有表示簡單句的符號和一些表示眞值函數聯結詞的符號，而且所謂簡單句是指相對於眞值函數聯結詞簡單的句子。基於這樣一個簡單理論，所謂形式當然是粗線條的。比如，按本章現有理論對下面的句子做符號化，

1. 所有的企鵝都是不會飛的鳥。
2. 張三相信，如果所有的企鵝都是不會飛的鳥，那麼他的家鄉就有不會飛的鳥。

其結果只是兩個表示簡單句的符號，但是這些句子的內部結構暗示着某種形式上的不同和聯繫。在§13.4.1（P.225）等章節中，我們會使用一個更豐富的邏輯分析理論來討論命題與論說的形式問題。

形式化的波蘭學派記法

如果一個形式語言的聯結詞用的是波蘭學派記法（見表 2.0），那麼這個語言就不需要括號。波蘭學派記法中一元聯結詞 $N$ 的使用規則和我們的 $\neg$ 一樣，但二元聯結詞 $K, A, C, E$ 的使用規則不同，它們都位於由它們聯結的兩個直接子公式的左側。具體地說，當我們使用波蘭學派記法時，公式的形成規則是下面這幾條（對比§2.3.0（P.79）中的形成規則和例子）：

1. 所有的命題變號都是公式；
2. 如果 $\varphi$ 是公式，那麼 $N \varphi$ 也是公式；
3. 如果 $\varphi$ 和 $\psi$ 是公式，那麼 $K\varphi\psi, A\varphi\psi, C\varphi\psi, E\varphi\psi$ 也是公式；
4. 只有這些是公式。

☯例 2.22 下面編號的都是公式而無編號的則都不是公式

1. $p_{156}$
2. $KNp_{75}p_{21}$
3. $Cp_9Ap_{57}Ep_{23}p_{601}$
4. $CCCCCp_{28}p_{28}p_{28}p_{28}p_{28}p_{28}$

• $Kp_{13}$
• $p_{822}Np_{822}$
• $p_{69}CNp_{801}$
• $Np_{28}Cp_{782}$

命題邏輯的基本語法

形式語言 $\mathscr{L_0}$

從這一節開始，我們要使用形式語言這一概念。命題邏輯的形式語言通常由兩部分組成：一是「初始符號」（primitive symbols），即無定義的符號；二是由這些符號根據一定的「形成規則」（formation rules）而形成的「公式」（formulas, formulae）。我們引入的第一個形式語言是 $\mathscr{L}_0.$

我們稱 $\mathscr{L}_0$ 的初始符號爲 $\mathscr{L}_0$-符號。$\mathscr{L}_0$-符號有三種：

1. 命題變號：$p_0$, $p_1$, $p_2, \cdots$;
2. 聯結詞：$\neg$, $\wedge$, $\vee$, $\rightarrow$, $\leftrightarrow$（$\neg$ 爲一元聯結詞，其餘爲二元聯結詞）；
3. 左右括號：($\hspace{2em}$).

$\mathscr{L}_0$-符號中，聯結詞 $\neg$, $\wedge$, $\vee$, $\rightarrow$, $\leftrightarrow$ 稱爲邏輯符號，命題變號稱爲非邏輯符號。命題變號也叫「命題變項」或「命題變元」。左右括號對於一個形式語言來說並不是必要的，但爲了方便，我們仍把它們作爲形式語言的初始符號，並稱它們爲「輔助符號」。

我們稱 $\mathscr{L}_0$ 的公式爲 $\mathscr{L}_0$-公式，它們是由 $\mathscr{L}_0$-符號根據下列形成規則形成的符號串：

1. $\mathscr{L}_0$ 的所有命題變號都是 $\mathscr{L}_0$-公式；
2. 如果 $\varphi$ 是 $\mathscr{L}_0$-公式，則 $\neg \varphi$ 也是 $\mathscr{L}_0$-公式；
3. 若 $\varphi$ 和 $\psi$ 是 $\mathscr{L}_0$-公式，則 $(\varphi \land \psi), (\varphi \lor \psi), (\varphi \rightarrow \psi), (\varphi \rightarrow \psi)$ 都是 $\mathscr{L}_0$-公式；
4. 只有這些是 $\mathscr{L}_0$-公式。

很多作者在我們用「公式」的地方用「合式公式」這個詞（“well-formed formula” 或 “wff”）。這裏用「公式」，是因爲這裏沒有不合式的公式。

根據上述定義，下列 $\mathscr{L}_0$-符號串都是 $\mathscr{L}_0$-公式：

1. $p_{156}$
2. $(\neg p_{75} \land p_{21})$
3. $(p_9 \rightarrow (p_{57} \lor (p_{23} \rightarrow p_{601})))$
4. $(((((p_{28} \rightarrow p_{28})\rightarrow p_{28})\rightarrow p_{28})\rightarrow p_{28})\rightarrow p_{28})$

下列 $\mathscr{L}_0$-符號串都不是 $\mathscr{L}_0$-公式：

1. $p_{13} \land$
2. $p_{822} \neg p_{822}$
3. $(p_{69} \rightarrow \neg p_{801}))$
4. $(p_{28} \neg \rightarrow p_{782}))$

爲了討論的方便，我們用 $p, q, r, s$ 等表示 $p_{0}, p_{1}, p_{2},…$ 中的前幾個（如果不對它們做限制），必要時可再用 $^\prime$, $^{\prime\prime}$ 或上下標來區分不同的命題變號。我們將用 $\varphi, \psi, \chi, \theta, \lambda$ 等小寫的希臘字母（加 $^\prime$, $^{\prime\prime}$ 或上下標）表示 $\mathscr{L}_0$-公式，用 $\Gamma, \Delta$ 等大寫的希臘字母表示 $\mathscr{L}_0$-公式集合。

對象語言和元語言

初學者要學會分清「對象語言」和「元語言」。所謂對象語言（object Ianguage），是作爲我們討論對象的語言；所謂元語言（metalanguage），是我們討論中使用的語言。比如，在一本英文敎科書裏，英文是對象語言。如果這本書是初級敎科書，那麼很可能中文就是元語言；而如果這本書是高級敎科書，那麼它的元語言很可能也是英文。在本書中，元語言是中文加上一些符號（偶爾還有一點英文），對象語言到目前爲止就是 $\mathscr{L}_0$。

注意：我們可以用 $\varphi$（或別的什麼符號）表示對象語言裏的某個公式（$\mathscr{L}_0$-公式），但那並不是說希臘字母 “$\varphi$” 是對象語言裏的符號或公式。"$\varphi$” 是我們元語言裏的符號，我們只是用它來表示某個 $\mathscr{L}_0$-公式。關於對象語言和元語言，現在只談這些，進一步的討論還會在§3.0.0（P.99）中出現。

這一章涉及的對象語言只有 $\mathscr{L}_0$，所以在提到 $\mathscr{L}_0$-公式或 $\mathscr{L}_0$-公式集時，我們將盡可能省略前綴 “$\mathscr{L}_0$"，只說公式或公式集。

子公式和主聯結詞

公式的子公式（subformula）是出現在該公式中的公式（包括它自己）。如果 $\psi$ 是 $\varphi$ 的子公式，且 $\psi \neq \varphi $，那麼 $\psi$ 是 $\varphi$ 的眞子公式（proper subformuIa）。一個公式的主聯結詞是該公式構造過程最後一步中使用的那個聯結詞，而它的直接子公式就是在這一步中主聯結詞聯結的公式。嚴格地說，

1. 對每個命題變號 $p$，$p$ 是 $p$ 的子公式；
2. $\varphi$ 的所有子公式和 $\neg \varphi$ 都是 $\neg \varphi$ 的子公式，$\varphi$ 是 $\neg \varphi$ 的直接子公式，且 $\neg$ 是 $\neg \varphi$ 的主聯結詞；
3. $\varphi$ 和 $\psi$ 的所有子公式和 $(\varphi \lor \psi)$ 都是 $(\varphi \lor \psi)$ 的子公式，$\varphi$ 和 $\psi$ 是 $(\varphi \lor \psi)$ 的直接子公式，且 $\vee$ 是 $(\varphi \lor \psi)$ 的主聯結詞；
4. $\varphi$ 和 $\psi$ 的所有子公式和 $(\varphi \land \psi)$ 都是 $(\varphi \land \psi)$ 的子公式，$\varphi$ 和 $\psi$ 是 $(\varphi \land \psi)$ 的直接子公式，且 $\wedge$ 是 $(\varphi \land \psi)$ 的主聯結詞；
5. $\varphi$ 和 $\psi$ 的所有子公式和 $(\varphi \rightarrow \psi)$ 都是 $(\varphi \rightarrow \psi)$ 的子公式，$\varphi$ 和 $\psi$ 是 $(\varphi \rightarrow \psi)$ 的直接子公式，且 $\rightarrow$ 是 $(\varphi \rightarrow \psi)$ 的主聯結詞；
6. $\varphi$ 和 $\psi$ 的所有子公式和 $(\varphi \leftrightarrow \psi)$ 都是 $(\varphi \leftrightarrow \psi)$ 的子公式，$\varphi$ 和 $\psi$ 是 $(\varphi \leftrightarrow \psi)$ 的直接子公式，且 $\leftrightarrow$ 是 $(\varphi \leftrightarrow \psi)$ 的主聯結詞；

以相同主聯結詞爲公式分類，我們有公式的下列類名稱：

1. 命題變號稱爲 $\mathscr{L}_0$-原子公式（atomic formula）；
2. 形如 $\neg \varphi$ 的公式（即以 $\neg$ 爲主聯結詞的公式）稱爲否定式（negation），俗稱「$\varphi$ 的否定」；
3. 形如 $(\varphi \lor \psi)$ 的公式稱爲析取式（disjunction），俗稱「$\varphi$ 和 $\psi$ 的析取」，$\varphi$ 和 $\psi$ 稱爲它的析取支（disjuncts）；
4. 形如 $(\varphi \land \psi)$ 的公式稱爲合取式（conjunction），俗稱「$\varphi$ 和 $\psi$ 的合取」。$\varphi$ 和 $\psi$ 稱爲它的合取支（conjuncts）；
5. 形如 $(\varphi \rightarrow \psi)$ 的公式稱爲蘊涵式（implication）或條件句（conditional），$\varphi$ 稱爲它的前件（antecedent），$\psi$ 稱爲它的後件（consequent）；
6. 形如 $(\varphi \leftrightarrow \psi)$ 的公式稱爲等值式（equivalence），亦稱雙（向）蘊涵式（bi-implication）或雙（向）條件句（biconditional）。

括號的省略

爲書寫和閱讀的方便，我們根據以下兩條規則省略公式中的一些括號：

1. 最外層的括號可以省略；
2. 假定 $\vee$ 和 $\wedge$ 的聯結比 $\rightarrow$ 和 $\leftrightarrow$ 優先，就像在做算術題時 $\times$ 和 $\div$ 比 $+$ 和 $-$ 優先（或者說 $\rightarrow$ 和 $\leftrightarrow$ 在做公式主聯結詞方面比 $\vee$ 和 $\wedge$ 優先）。

☯例 2.23 下列符號串不是省略了括號的公式

1. $p \land q \lor r$
2. $p \rightarrow q \rightarrow r$
3. $p \rightarrow q \lor r \rightarrow s$
4. $p \rightarrow (q \lor r) \rightarrow s$
5. $p \rightarrow q \rightarrow r \lor s$

☯例 2.24 編號者爲省略括號的公式，未編號者爲對應未省略括號的公式

1. $(p \rightarrow q) \land r$
2. $p \land q \rightarrow \neg r \land s$
3. $p \lor q \rightarrow \neg(p \land q)$
4. $(p \lor q) \land r \rightarrow s$
5. $((p \rightarrow q) \rightarrow r) \rightarrow s$

• $((p \rightarrow q) \land r)$
• $((p \land q) \rightarrow (\neg r \land s))$
• $((p \lor q) \rightarrow \neg(p \land q))$
• $(((p \lor q) \land r) \rightarrow s)$
• $(((p \rightarrow q) \rightarrow r) \rightarrow s)$

注意：一個符號串是否爲省略了括號的公式，取決於特定作者或特定書籍對省略括號的約定。根據本書的約定，例 2.24 中（編號者）的符號串是公式而例 2.23 中的不是。但若按照其他約定，例 2.24 中的有可能不是公式而例 2.23 中的倒有可能是公式。比如，有的作者喜歡「右結合原則」，卽同一種聯結詞連續出現時，右邊的聯結詞比左邊的優先。在這一約定下，例 2.23 中的第二個符號串就成了公式 $(p \rightarrow (q \rightarrow r))$ 的省略括號的寫法。如果在我們上述約定的基礎上再加「右結合原則」，那麼例 2.23 中的第三個符號串也就成了公式 $(p \rightarrow ((q \lor r) \rightarrow s))$ 省略括號的寫法。當然，還有很多不同的約定方法，這裏就不一一介紹了。

語法和語義

語法（syntax）和語義（semantics）的區別對學習當代邏輯至關重要。語法理論有時叫語形理論，它涉及符號組合和公式的結構，以及公式在結構或形式方面的各種關係，唯獨不涉及這些符號和公式的意義。討論符號和公式意義的理論稱爲語義理論。本節的上述內容和以後將討論的公式的變換、公式序列（依規則）的生成等，都屬於語法理論。

有時人們談論有意義的符號和無意義的符號。在邏輯學家們的筆下，「符號」多數時候是指沒有被賦予意義的東西。比如，前面討論的符號本身都是沒有意義的。一旦賦予這些符號意義，我們就進入了語義理論。針對符號和公式的意義的討論，包括公式的眞假，統稱爲語義討論。

爲理解語法和語義的區別，我們來看下面幾個表達式：

1. $1+1=2$
2. One pIus one is (equal to) two.
3. 一加一等於二。

這些是不同語言中的句子，而不同語言有不同的符號和形成規則。（自然語言很難說有嚴格的形成規則，但大體上是有規則的。）所以，這些句子從語法上說是不同的。但是，根據通常的解釋，它們的意思是相同的，或者說在語義上是相同的。再來看同一個語言中的例子：

1. 張三打了李四一拳。
2. 李四被張三打了一拳。

顯然這兩個句子的意思相同，即在語義方面相同。但是，第一句有八個字，而第二句卻有九個字；第一句的前兩個字是「張三」，而第二句的前兩個字卻是「李四」。所以，這兩個句子在語法方面是不同的。

基本眞值表和眞值的計算

在這一節裏，我們介紹眞值表和公式眞值的計算方法，然後在下一節用這種方法來討論命題邏輯的一些基本語義概念。

聯結詞的語義解釋

命題邏輯不涉及命題中不能由聯結詞表現出來的內部結構，所以在某種意義上說，命題邏輯是研究聯結詞的。

從語法角度看，聯結詞自然是「公式函數」，即從公式集合到公式集合的函數。這就是說，對每個聯結詞，每當給出公式作爲「輸入」，這個聯結詞確定了唯一的公式作爲「輸出」，即以該聯結詞爲主聯結詞並以給定公式爲直接子公式的公式。那麼，諸如「並非」「並且」這樣的聯結詞的意義（meaning）又是什麼呢？我們說過，這些聯結詞是眞值函數聯結詞。什麼是眞值函數（truth function）？眞值函數是從眞值集到眞值集的函數。我們用 T 或 1 表示眞，用 F 或 0 表示假。根據我們對眞值的「二值」預設，眞值函數就是從 $\lbrace 1, 0\rbrace $ 到 $\lbrace 1, 0\rbrace $ 的函數。眞值函數聯結詞之所以叫「眞值函數聯結詞」，是因爲從語義角度看，它們是眞值函數。換句話說，眞值函數聯結詞就是以眞值函數爲其解釋的聯結詞。關於這一點，我們在§3.3.0（P.115）和§3.5（P.122）中還會討論。

現在，我們先用比較直觀的眞值表（truth table）來討論眞值函數聯結詞。表 2.1 是關於五個眞值函數聯結詞的基本眞值表。

Table 2.1: 基本真值表 $$ \begin{array}{cc|ccccc} \hline \hline \varphi & \psi & \varphi \wedge \psi & \varphi \vee \psi & \varphi \rightarrow \psi & \varphi \leftrightarrow \psi & \neg \varphi \\ \hline 1 & 1 & 1 & 1 & 1 & 1 & 0 \\ 1 & 0 & 0 & 1 & 0 & 0 & \\ 0 & 1 & 0 & 1 & 1 & 0 & 1 \\ 0 & 0 & 0 & 0 & 1 & 1 & \\ \hline \hline \end{array} $$

根據表 2.1，無論 $\varphi$ 是怎樣的公式，如果 $\varphi$ 是眞的， $\neg \varphi$ 就是假的；如果 $\varphi$ 是假的，$\neg \varphi$ 就是眞的。這就是說，$\neg \varphi$ 的眞值完全取決於 $\varphi$ 的眞值。類似地，無論 $\varphi$ 和 $\psi$ 是什麼公式，如果 $\varphi$ 和 $\psi$ 都是眞的，$\varphi \rightarrow \psi$ 就是眞的；如果 $\varphi$ 是眞的而 $\psi$ 是假的，$\varphi \rightarrow \psi$ 是假的；……用 $\land, \lor, \leftrightarrow$ 做主聯結詞的情況依此類推。

因爲每個公式 $\varphi$ 都是由命題變號經五個眞值函數聯結詞構造出來的，所以，一旦 $\varphi$ 中命題變號的眞值確定了，$\varphi$ 的眞值就可以按照上述基本眞值表一步步計算出來。

在計算公式的眞值前，先把基本眞值表 2.1 記住，就像做乘法運算前要先記住乘法口訣那樣。記眞值表時要記住這些組合情況與右側眞值的對應，僅僅簡單地記住「合取：1, 0, 0, 0；析取：1, 1, 1, 0；…」並不是好辦法，甚至可能導致誤解。嘗試記住下列命題：

1. 一個否定式是眞的，當且僅當它否定的公式是假的；
2. 一個合取式是眞的，當且僅當它的合取支都是眞的；
3. 一個析取式是眞的，當且僅當它的析取支中至少有一個是眞的；
4. 一個蘊涵式是眞的，當且僅當它的前件是假的或後件是眞的；
5. 一個等值式是眞的，當且僅當它的兩個直接子公式的眞值相同。

由此，可以對應地得岀命題「一個否定式是假的，當且僅當它否定的公式是眞的」等等。讀者應試着把餘下的幾個對應命題找出來，見練習 2.3。

公式眞值的計算

公式眞值的計算方法分兩類，一是用子公式的給定眞值來計算公式的眞值，二是用公式的眞值表計算公式在各種可能情況下的眞值。

以子公式的給定眞值計算

我們先看如何用命題變號的給定眞值來計算公式的眞值。

一個公式的眞值的計算未必要從它的原子子公式開始——計算可以從它的其他子公式開始。比如，

☯例 2.26
設 $\varphi$ 的眞值爲 1，$\psi$ 的眞值爲 0 並且 $\chi$ 的眞值爲 0. 計算公式 $(\varphi \rightarrow \neg \psi \land \chi) \rightarrow (\varphi \lor \chi)$ 的眞值。
解：與例 2.25 解法相同，易知其眞值爲 1.

例 2.25, 2.26 使我們明白：要計算出一個公式的眞值，我們只需知道它的所有直接子公式的眞值，而不一定要知道它的所有原子子公式的眞值。其實，要計算出一個公式的眞值，也未必要事先知道它的所有直接子公式的眞值。

☯例 2.27
設 $\varphi$ 的眞值爲 1 且 $\psi$ 的眞值爲 0. 那麼對任意公式 $\chi$，根據（眞值）表 2.1，以下結論是顯然的：

1. $\varphi \lor \chi$ 的眞值爲 1，
2. $\chi \rightarrow \varphi$ 的眞值爲 1，
3. $\chi \land \psi$ 的眞值爲 0，
4. $\psi \rightarrow \chi$ 的眞值爲 1.

☯例 2.29
設 $\psi$ 眞值爲 0. 計算公式 $\psi_{0} \rightarrow\left(\psi_{1} \rightarrow\left(\psi_{2} \rightarrow(\chi \wedge \psi \rightarrow \xi)\right)\right)$ 的眞值。
解：原理與方法與前幾例並無區別。易知 $\chi \wedge \psi$ 眞值爲 0，則 $\chi \wedge \psi \rightarrow \xi$ 眞值爲 1，那麼無論前件眞值爲 1 或 0，公式眞值始終爲 1.

以公式的眞值表計算

一旦會用子公式的眞值來計算公式的眞值，構造公式的眞值表是件很簡單的事——它不過是列出給定公式中的全部命題變號的所有「可能取值組合」，並根據它們計算和列出該公式在每一種可能情況下的眞值。

對給定公式中的每個命題變號指定一個固定的眞值，這樣指定的結果稱爲這些命題變號的一個「可能取值組合」。若干命題變號的一個可能取值組合是從這些命題變號到 $\lbrace 1,0\rbrace $ 的一個函數。因爲每個命題變號的眞值或爲 1 或爲 0，則 $n$ 個命題變號的可能取值組合爲 $2^n$ 個。一個公式的眞值表一定要包含該公式中命題變號的所有可能取值組合。在構造公式 $\varphi$ 的眞值表時，按慣例先在表的左側排出 $\varphi$ 中出現的所有命題變號，然後排列出它們的全部可能取值組合（的值），再把 $\varphi$ 的各個子公式的眞值從簡單到複雜一步步計算出來。

公式的眞值表通常有兩種畫法，第一種是在表的上方排出該公式的所有子公式，通過計算將這些子公式的眞值列在它們的下方。

公式的眞值表的第二種畫法是在表上方只列出該公式（及其原子子公式），而把它的（非原子）子公式的值列在該子公式的主聯結詞之下。

例 2.31 有意將公式中符號間的距離加大，以使讀者清楚地看出：每個子公式的眞值都列在該子公式的主聯結詞的下方。特別地，例 2.31 中「$\rightarrow$」之下那列眞值，是公式 $(p \vee q) \wedge \neg r \rightarrow p \wedge (\neg q \vee r)$ 在各種情況下的眞值。我們將一貫地將子公式的眞值列於該子公式的主聯結詞之下，但不再加大公式中符號間的距離。從現在起，將只釆用公式眞值表的第二種畫法。

我們約定：凡談到眞值表中的眞值時，我們用「行」表示該表中從左到右的眞值序列，用「列」表示該表中從上到下的眞值序列。

若干基本語義概念的眞值表刻畫

這一節裏，我們用眞值表方法介紹和討論一些基本語義概念：重言蘊涵（重言後承）、重言等值、可滿足性、重言式、矛盾式和或然式。我們對這些概念所做的眞值表刻畫，在某些敎科書中就稱爲這些概念的定義。之所以我們不稱這些刻畫爲定義，是因爲這裏的討論不夠嚴格。在§3.1（P.101）中，我們要用眞值指派給出這些概念的嚴格定義。

爲了比較和討論不同公式的眞值情況，我們可以把不同的公式放到同一個眞值表中。這樣的眞值表稱爲聯合眞值表。在公式 $\varphi_0,…\varphi_n$ 的聯合眞值表中，我們要列出這些公式的所有原子子公式和它們的可能取值組合（的值），並且根據這些組合計算 $\varphi_0,…\varphi_n$ 各自的眞值。

論說形式的有效性

一個論說形式的前提和結論的聯合眞值表稱爲該論說形式的眞值表。有了論說形式的眞值表，引言中討論的論說形式的好壞可以有更清楚的定義（下面的「有效」對應於「好」，「無效」對應於「壞」；參見§0.0（P.2）和§2.2（P.76）中的有關形式好壞的討論。）

1. 在一個論說形式的眞值表中，前提都眞而結論假的每一行，都稱爲該論說形式的反例。
2. 對任何一個論說形式，如果其眞值表的任何一行都不是該論說形式的反例，那麼這個論說形式是有效的（valid）；否則，這個論說形式是無效的（invalid）。

讀者在這裏可能會有這樣一個問題：我們在引言裏曾說過，論說形式的好壞涉及該形式的所有特例，其數量顯然無上界；而這裏說的論說形式的有效性卻只涉及 $2^n$ 個可能的取值組合（假設其中只出現 $n$ 個命題變號）。這兩種說法如何能是「一回事」呢？

可以這樣來理解這個問題：假定一個論說形式中出現 $n$ 個命題變號，進而該論說形式的眞值表有 $2^n$ 行。這個論說形式的每個特例，都可以看作是以具體命題替換那些命題變號而得到的。替換的都是具體命題，因而它們的眞值都是確定的，對應於 $2^n$ 個可能取值組合中的一個。（${\prod_{i=1}^{n}} (C_{2}^{1})_i = 2^{n}.$）這樣，我們就把該論說形式的所有特例分成了 $2^n$ 組，而每個特例的前提和結論的眞值情況，都在該論說形式眞值表的某一行中。當討論這個眞值表的任一行時，假如沿用引言中的術語，那麼我們就會說，討論涉及該論說形式的一組特例而非一個特例；當我們認定眞值表的某一行是給定論說形式的反例時，假如沿用引言中的術語，那麼我們就會說該論說形式有一組反例。

重言蘊涵

設 $\varphi_0,…,\varphi_n$ 和 $\psi$ 爲任意公式。$\lbrace \varphi_0,…,\varphi_n \rbrace $ 重言蘊涵（tautologically implies） $\psi$ 當且僅當在 $\varphi_0,…,\varphi_n$ 與 $\psi$ 的聯合眞值表中，沒有一行是 $\varphi_0,…,\varphi_n$ 都眞而 $\psi$ 假，亦即在它們的聯合眞值表的每一行中，如果 $\varphi_0,…,\varphi_n$ 的眞值都是 1，那麼 $\psi$ 的眞值也一定是 1. $\psi$ 是$\lbrace \varphi_0,…,\varphi_n \rbrace $ 的重言後承（tautological consequence）當且僅當 $\varphi_0,…,\varphi_n$ 重言蘊涵 $\psi$.（$\lbrace \varphi_0,…,\varphi_n \rbrace $ tautologically implies $\psi$）

易見，根據有效性和重言蘊涵的定義，下列兩個命題等價：

1. $\lbrace \varphi_0,…,\varphi_n \rbrace $ 重言蘊涵 $\psi$，
2. 以 $\varphi_0,…,\varphi_n$ 爲前提並以 $\psi$ 爲結論的論說形式是有效的。

在理論討論中，「重言蘊涵」比「有效論說形式」使用得更多，儘管根據上述等價性，我們知道在命題邏輯部分，它們說的是一回事。（這裏談到的公式集合都是有窮集合，無窮集合的情況將在§3.1（P.101）中討論。在謂詞邏輯部分，重言蘊涵關係將讓位於邏輯蘊涵關係，重言後承關係將讓位於邏輯後承關係。）

☯例 2.35
$\lbrace p \rightarrow (q \rightarrow r), p \rightarrow q \rbrace $ 重言蘊涵 $p \rightarrow r$，而 $r \rightarrow \neg q$ 則不是 $\lbrace p \rightarrow q \lor \neg r, r \land q \rightarrow p \rbrace $ 的重言後承。
解：分別見例 2.33 和例 2.34 中的眞值表。

重言等值

設 $\varphi$ 和 $\psi$ 爲任意公式。$\varphi$ 與 $\psi$ 重言等值（tautologically equivalent） 當且僅當在 $\varphi$ 與 $\psi$ 聯合眞值表的任意一行中，$\varphi$ 與 $\psi$ 有同樣的眞值，亦即在它們的聯合眞值表的每一行中，如果 $\varphi$ 的眞值是 1，則 $\psi$ 的眞值也是 1；並且如果 $\varphi$ 的眞值是 0，則 $\psi$ 的眞值也是 0.

根據重言蘊涵和重言等值的定義，易見下列命題等價：

1. $\varphi$ 與 $\psi$ 重言等值，
2. $\varphi$ 與 $\psi$ 相互重言蘊涵（$\varphi$ 與 $\psi$ 各是對方的重言後承）。

可滿足性

這裏說的可滿足性（satisfiability），就是§0.2（P.8）中說的語義一致性。設 $\Gamma$ 爲任意有窮的公式集合。$\Gamma$ 是可滿足的（satisfiable）當且僅當 $\Gamma$ 中公式的聯合眞值表中存在某一行，在該行裏 $\Gamma$ 中的公式的眞值都是 1. $\Gamma$ 是不可滿足的當且僅當它不是可滿足的。設 $\varphi$ 爲任意公式。$\varphi$ 是可滿足的當且僅當 $\lbrace \varphi\rbrace $ 是可滿足的。$\varphi$ 是不可滿足的當且僅當 $\lbrace \varphi\rbrace $ 不是可滿足的。

我們簡要地介紹一些關於可滿足性的命題，部分涉及可滿足性與重言蘊涵的關係。這些命題都有簡單的證明，其中一部分會在§3.1（P.101）中討論。請讀者思考這些命題成立的理由（見習題 2.17）。

設 $\Gamma = \lbrace \varphi_0,…,\varphi_n\rbrace $ 爲任意有窮的公式集，$\varphi$ 爲任意公式。我們有：

1. 如果 $\Gamma$ 可滿足，那麼對任何公式集 $\Delta$，$\Gamma \cap \Delta$ 也可滿足。（注：對所有集合 $X$ 和 $Y$，$X \cap Y = \lbrace x: x \in X \text{且} x \in Y \rbrace $，它是包含 $X$ 和 $Y$ 的所有公共元素的集合，稱爲 $X$ 和 $Y$ 的交（intersection）。）
2. 如果 $\Gamma$ 不可滿足，那麼對任何有窮公式集 $\Delta$，$\Gamma \cup \Delta$ 也不可滿足。（注：對所有集合 $X$ 和 $Y$，$X \cup Y = \lbrace x: x \in X \text{或} x \in Y \rbrace $，它是包含 $X$ 的所有元素和 $Y$ 的所有元素的集合，稱爲 $X$ 和 $Y$ 的並集（union）。）
3. 設 $\Gamma \subseteq \Delta$，其中 $\Delta$ 是任意有窮公式集。如果 $\Delta$ 可滿足則 $\Gamma$ 可滿足（如果 $\Gamma$ 不可滿足則 $\Delta$ 不可滿足）。（注：對所有集合 $X$ 和 $Y$，$X \subseteq Y$ 當且僅當 $X$ 的所有元素都是 $Y$ 的元素，$X \subset Y$ 當且僅當 $X \subseteq Y$ 並且 $Y \nsubseteq X$（並非 $Y \subseteq X$）。當 $X \subseteq Y$，我們稱 $X$ 是 $Y$ 的子集（subset），也稱 $Y$ 是 $X$ 的擴集（superset）或擴充（extension）。當 $X \subset Y$，我們稱 $X$ 是 $Y$ 的眞子集（proper subset），也稱 $Y$ 是 $X$ 的眞擴集或眞擴充。注意：「$X \subseteq Y$」表達的是個命題，說的是 $X$ 和 $Y$ 之間的某種關係；而「$X \cap Y$」「$X \cup Y$」和下面的「$X - Y$」不表達命題，只表示 $X$ 和 $Y$ 在某些運算下的值——集合。）
4. $\Gamma \cup \lbrace \neg \varphi\rbrace $不可滿足當且僅當 $\Gamma$ 重言蘊涵 $\varphi$。
5. 對任意 $i \leqslant n$，$\Gamma$ 不可滿足當且僅當 $\Gamma - \lbrace \psi_i\rbrace $ 重言蘊涵 $\neg \psi_i$。（注：對所有集合 $X$ 和 $Y$，$X - Y = \lbrace x: x \in X \text{且} x \notin Y \rbrace $，它是包含 $X$ 的所有元素但不包含 $Y$ 的任何元素的集合，稱爲 $X$ 和 $Y$ 的差（difference），也稱爲 $Y$ 在 $X$ 中的相對補（relative complement of $Y$ in $X$）。）
6. 如果 $\Gamma$ 不可滿足，那麼 $\Gamma$ 重言蘊涵 $\varphi$。
7. 如果 $\neg \varphi$ 不可滿足，那麼 $\Gamma$ 重言蘊涵 $\varphi$。
8. 如果 $\Gamma$ 重言蘊涵 $\varphi$，並且 $\Gamma$ 可滿足，那麼 $\varphi$ 也可滿足。
9. 如果 $\Gamma$ 重言蘊涵 $\varphi$ 並且 $\Gamma$ 重言蘊涵 $\neg \varphi$，那麼 $\Gamma$ 不可滿足。

重言式、矛盾式與或然式

根據公式在其眞值表各行中的眞值情況，我們把公式分成三類：重言式（tautology）、矛盾式（contradiction）與或然式（偶然式，contingency）。

1. 公式 $\varphi$ 是重言式（tautology）當且僅當在其眞值表的每一行中，$\varphi$ 的眞值都是 1，即 $\varphi$ 總是眞的。
2. 公式 $\varphi$ 是矛盾式（contradiction）當且僅當在其眞值表的每一行中，$\varphi$ 的眞值都是 0，即 $\varphi$ 總是假的。（矛盾式也稱不可滿足式。）
3. 公式 $\varphi$ 是或然式（contingency）當且僅當在其眞值表中，$\varphi$ 的眞值在某些行中是 1，而在另一些行中是 0，即 $\varphi$ 有時眞有時假。

類似於討論可滿足性與重言蘊涵時的情況，我們只簡要介紹些關於重言式、矛盾式與或然式之間的關係的命題，其中一部分會在§3.1.3（P.104）中討論。請讀者思考下列命題成立的理由（另見習題 2.6-2.9）。

1. 重言式的否定是矛盾式。
2. 矛盾式的否定是重言式。
3. 或然式的否定還是或然式。
4. 重言式與重言式的合取是重言式。
5. 重言式與矛盾式的合取是矛盾式。
6. 重言式與或然式的合取是或然式。
7. 矛盾式與矛盾式的合取是矛盾式。
8. 矛盾式與或然式的合取是矛盾式。
9. 或然式與或然式的合取或者是或然式，或者是矛盾式。

關於上面引入的各語義概念間的關係，我們同樣只簡單介紹而不做證明。另一些命題將在§3.1（P.101）中討論。

易見，對所有公式 $\varphi, \psi, \chi$，%公式 $\varphi \land (\psi \land \chi)$ 與 $(\varphi \land \psi) \land \chi$ 重言等值，公式 $\varphi \lor (\psi \lor \chi)$ 與 $(\varphi \lor \psi) \lor \chi$ 重言等值。

1. $\varphi \land (\psi \land \chi)$ 與 $(\varphi \land \psi) \land \chi$ 重言等值
2. $\varphi \lor (\psi \lor \chi)$ 與 $(\varphi \lor \psi) \lor \chi$ 重言等值

以下，我們省略一連串合取和一連串析取應有的括號，用 $\varphi_{0} \wedge \cdots \wedge \varphi_{n}$ 表示 $\left(\cdots\left(\varphi_{0} \wedge \varphi_{1}\right) \wedge \cdots \wedge \varphi_{n-1}\right) \wedge \varphi_{n}$，用 $\varphi_{0} \vee \cdots \vee \varphi_{n}$ 表示 $\left(\cdots\left(\varphi_{0} \vee \varphi_{1}\right) \vee \cdots \vee \varphi_{n-1}\right) \vee \varphi_{n}$。在極限情況 $n=0$ 時，$\varphi_{0} \wedge \cdots \wedge \varphi_{n}= \varphi_{0} \vee \cdots \vee \varphi_{n}=\varphi_{0}$。這就是說，當 $\varphi_{0} \wedge \cdots \wedge \varphi_{n}$ 或 $\varphi_{0} \vee \cdots \vee \varphi_{n}$ 在討論中出現而我們又要考慮主聯結詞時，我們可以按「左結合」的原則恢復括號。

設 $\varphi, \psi, \varphi_{0},…,\varphi_{n}$ 爲任意公式且 $\Gamma = \lbrace \varphi_{0},…,\varphi_{n}\rbrace $。請思考下列命題成立的理由（見習題 2.18）：

1. $\varphi$ 重言蘊涵 $\psi$ 當且僅當 $\varphi \rightarrow \psi$ 是重言式；
2. $\varphi$ 重言等值於 $\psi$ 當且僅當 $\varphi \rightarrow \psi$ 是重言式，當且僅當 $\psi \rightarrow \varphi$ 與 $\varphi \rightarrow \varphi$ 都是重言式；
3. $\Gamma$ 重言蘊涵 $\psi$ 當且僅當 $\varphi_{0} \land \cdots \land \varphi_{n} \rightarrow \psi$ 是重言式；
4. $\varphi_{0} \land \cdots \land \varphi_{n} \rightarrow \psi$ 與 $\varphi_{0} \land \cdots \land \varphi_{n-1} \rightarrow (\varphi_n \rightarrow \psi )$ 重言等值；
5. 如果 $\varphi$ 是重言式，那麼 $\Gamma$ 重言蘊涵 $\varphi$；
6. $\Gamma$ 可滿足當且僅當 $\varphi_{0} \land \cdots \land \varphi_{n}$ 或者是或然式或者是重言式；
7. $\Gamma$ 不可滿足當且僅當 $\varphi_{0} \land \cdots \land \varphi_{n}$ 或者是或然式或者是矛盾式。
8. 如果 $\varphi$ 是重言式，那麼 $\Gamma$ 是可滿足的當且僅當 $\Gamma \cup \lbrace \varphi\rbrace $ 是可滿足的；
9. 如果 $\varphi_i (i \leqslant n)$ 是重言式，那麼 $\Gamma$ 是可滿足的當且僅當 $\Gamma - \lbrace \varphi_i\rbrace $ 是可滿足的；
10. 如果 $\varphi$ 是矛盾式，那麼 $\Gamma \cup \lbrace \varphi\rbrace $ 是不可滿足的；
11. 如果 $\varphi_i (i \leqslant n)$ 是矛盾式，那麼 $\Gamma$ 是不可滿足的。

簡化眞值表方法

我們知道，如果對一個包含 $n$ 個命題變號的公式構造完整的真值表，其真值表有 $2^n$ 行。隨着 $n$ 的增長，$2^n$ 是以「指數」增長的。藉助計算機，假定以 $100,0000$ 行每秒的速度生成真值表，當 $n=80$ 時，那就需要 $2^{80} \mu \mathrm{s}$ 生成真值表，這個時間是多長呢？換算成以年爲單位的話，大槪是 $380$ 億年，而宇宙至今也只存在了大槪 $150$ 億年，超過了宇宙到現在的存在時間！這也是現代理論計算機科學中最著名的難題。［Enderton,2001: 25］

所以，一旦公式（集）中出現 3 個或更多的命題變號，它們的真值表就會比較大，手工畫起來常有困難。日常思維與語言中的論證，涉及的命題變號通常並不多，可以引入簡化真值表方法判定一個論説形式是否有效。簡化真值表方法有多種，這裏只介紹其一。

用簡化眞值表法判別一個論說形式是否有效，通常可按以下方式來做：首先假設該論說形式的前提都眞而結論假，然後根據它們的眞值算出它們的直接子公式的眞值，再進一步根據子公式的眞值算出這些子公式的直接子公式的眞值。（當遇到合取式爲假或析取式爲眞等情況時，不能直接算出它們的直接子公式的眞值而要分情況討論。）在這一過程中，若遇到某公式既眞又假，就可判定給出的論說形式是有效的；若沒有遇到這種情況，則可判定該論說形式是無效的。在後一種情況下，能找到該論說形式中命題變號的一個可能取值組合，使得根據這個組合，該論說形式的前提爲眞而結論爲假。

由於重言蘊涵和有效論說形式是「一回事」，所以我們就不再單獨討論如何用簡化眞值表方法判定一個公式集是否重言蘊涵某個公式。

要說明一個公式是重言式，我們可以假設它爲假，再試圖說明這不可能；而一旦這個假設沒有導致矛盾，那麼我們就會得到命題變號的一個可能取值組合，使得給定公式爲假。類似地，要說明一個公式是矛盾式，我們可以假定它是眞的，再試圖說明這不可能；而一旦這個假設沒有導致矛盾，那麼我們就會得到命題變號的一個可能取值組合，使得給定公式爲眞。如果假設一公式爲眞沒有導致矛盾，並且假設它爲假也沒有導致矛盾，那麼該公式就一定是或然式。

在例 2.48 中，我們的思路是：在已確定 $\neg(p \rightarrow r), q \rightarrow \neg p, \neg q \rightarrow \neg p$ 都爲眞時，選擇蘊涵式的否定 $\neg(p \rightarrow r)$ 來進一步求得蘊涵式前件 $p$ 的眞值 1. 假如我們選擇的是蘊涵式 $q \rightarrow \neg p$ 或 $\neg q \rightarrow \neg p$，那麼我們就不得不分情況討論，因爲當時只能得到：或者其前件是假的或者其後件是眞的。顯然，選擇 $\neg(p \rightarrow r)$ 以求得 $p$ 的眞值 1，使我們避免了「分情況討論」的複雜局面。這裏運用了下述「經驗規則」：

如果在某一步驟中得到 $\neg (\varphi \lor \psi)$ 或 $\neg (\varphi \rightarrow \psi)$ 的眞值爲 1（或得到 $\varphi \lor \psi$ 或 $\varphi \rightarrow \psi$ 的眞值爲 0），先用這一信息求得子公式 $\varphi$ 和 $\psi$ 的眞值。這樣做往往可以簡化確定其他子公式眞值的過程。

運用簡化眞值表的方法，我們同樣可以說明一個公式是或然式、非重言式或者非矛盾式等。具體例子省略，請讀者去做練習。

第三章開始學習寫證明。簡化眞值表方法雖然並不就是寫證明，但它們的思路有時是類似的。從現在起應注意與證明有關的問題。

本章習題

習題 2.0：說明下列聯結詞不是眞值函數聯結詞

1. 因爲$\underline{\hspace{3em}}$，所以$\underline{\hspace{3em}}$。
2. 可以想像$\underline{\hspace{3em}}$。
3. 昨天$\underline{\hspace{3em}}$。
4. 張三相信$\underline{\hspace{3em}}$。
5. 李四認爲$\underline{\hspace{3em}}$。
6. 王五知道$\underline{\hspace{3em}}$。
7. 政客們喜歡說$\underline{\hspace{3em}}$。
8. 從平民的角度看$\underline{\hspace{3em}}$。

習題 2.1：給出「辭典」，並將下列語句符號化

1. 不是所有的人都講道理。
2. 如果在選舉時你不去投票，那麼你就要忍受我選的白癡。
3. 張三是李四的祖先當且僅當李四是張三的後代。
4. 除非有奇蹟出現，中國足球隊 500 年內擠不進世界 16 強。
5. 張三只有堅持鍛鍊纔會有好身體；但並非只要他堅持鍛鍊就會有好身體。
6. 如果張三一進大學就知道自己想做什麼，那麼，他大學期間不會浪費太多時間，而他的學習成績也不會太差。
7. 要麼明天有海戰，要麼明天沒有海戰；但明天不必然有海戰，而且明天也不必然沒有海戰。

習題 2.2：給出「辭典」，將下列論說符號化，判斷是否有效並給出理由

1. 如果今天是星期三，那麼明天有邏輯課。因此，如果明天沒有邏輯課，則今天不是星期三。
2. 要麼士兵拿破崙想當將軍，要麼士兵拿破崙不想當將軍。如果士兵拿破崙想當將軍，那麼他不是一個好士兵。如果士兵拿破崙不想當將軍，那麼他也不是一個好士兵。所以，士兵拿破崙不是一個好士兵。
3. 或者邏輯難學，或者沒有多少學生喜歡它。如果數學容易學，那麼邏輯不難學。因此，如果許多學生喜歡邏輯，那麼數學並不容易學。
4. 如果上帝死了，那麼做什麼壞事情都是可以的。如果做什麼壞事情都是可以的，那麼我考試作弊也是可以的。所以，如果上帝死了，我考試作弊是可以的。
5. 花都是紅的當且僅當李四不是色盲。花不都是紅的。所以李四是色盲。
6. 如果 $a$ 是正整數，則 $a$ 有唯一的後繼，並且 $a$ 有唯一的前驅。$a$ 要麼並非有唯一的後繼，要麼並非有唯一的前驅。所以 $a$ 不是正整數。
7. 如果我相信上帝，則如果上帝是存在的，我就有所得；如果上帝不存在，我也無所失。另一方面，如果我不相信上帝，則如果上帝存在，我有所失；如果上帝不存在，我無所得。因此，我如果相信上帝，我或者有所得，或者無所失；而如果我不相信上帝，則我或者有所失，或者無所得。
8. 分析示例 32.1（P.427）中荊王免去士兵死罪的推理過程，並加以符號化。

習題 2.3：填寫空格，使下列命題都成立

1. 一個否定式是假的當且僅當$\underline{\hspace{5em}}$；
2. 一個合取式是假的當且僅當$\underline{\hspace{5em}}$；
3. 一個析取式是假的當且僅當$\underline{\hspace{5em}}$；
4. 一個蘊涵式是假的當且僅當$\underline{\hspace{5em}}$；
5. 一個等值式是假的當且僅當$\underline{\hspace{5em}}$。

習題 2.4：給出下列公式的眞值表

1. $\neg \neg p \rightarrow p$
2. $ p \rightarrow(\neg p \rightarrow q) $
3. $p \rightarrow p \wedge q$
4. $ p \wedge q \rightarrow p \vee q$
5. $p \vee q \rightarrow p \wedge q $
6. $p \vee q \rightarrow \neg(p \rightarrow q$
7. $p \wedge q \rightarrow \neg(p \rightarrow \neg q)$
8. $(p \rightarrow q) \rightarrow \neg(\neg q \rightarrow \neg p)$
9. $\neg(p \vee q) \rightarrow \neg p \wedge \neg q$
10. $\neg(p \wedge q) \rightarrow \neg p \vee \neg q$
11. $(p \rightarrow q) \vee(q \rightarrow p) $
12. $(\neg p \rightarrow q) \rightarrow((\neg p \rightarrow \neg q) \rightarrow p) $
13. $(p \rightarrow(q \rightarrow r)) \rightarrow((r \rightarrow q) \rightarrow(r \rightarrow p))$
14. $(p \leftrightarrow q) \leftrightarrow \neg(p \wedge q) \vee \neg(\neg p \wedge \neg q)$
15. $(p \vee q) \wedge(p \vee r) \rightarrow p \vee(q \wedge r)$

習題 2.5：判斷下列說法的對錯，並說明理由

1. 任一公式都或者是重言式，或者是矛盾式，或者是或然式；並且只能是這三種公式中的一種。
2. 對任意公式集 $\Gamma$ 和任意公式 $\varphi$，$\Gamma$ 或者重言蘊涵 $\varphi$ 或者重言蘊涵 $\neg \varphi$。
3. 對任意公式 $\varphi$ 和 $\psi$，$\varphi$ 或者與 $\psi$ 重言等價或者與 $\neg \psi$ 重言等價。
4. 對任意公式 $\varphi$，或者 $\varphi$ 可滿足或者 $\neg \varphi$ 可滿足。

習題 2.6：判斷下列說法的對錯
在每個括號中畫 $\checkmark$ 或 ✗ 分別表明「可以是」和「一定不是」，並思考原因。如或然式與或然式的合取：（✗）重言式，（$\checkmark$）矛盾式，（$\checkmark$）或然式。它相當於說：或然式與或然式的合取可以是矛盾式，也可以是或然式，但一定不是重言式。（當然，如果正確的畫法中有兩個 ✗，那麼第三個一定是畫 $\checkmark$，而且畫 $\checkmark$ 的地方一定可以讀作「一定是」。想想爲什麼是這樣。

1. 重言式與重言式的析取：（$\underline{\hspace{1em}}$）重言式，（$\underline{\hspace{1em}}$）矛盾式，（$\underline{\hspace{1em}}$）或然式。
2. 重言式與矛盾式的析取：（$\underline{\hspace{1em}}$）重言式，（$\underline{\hspace{1em}}$）矛盾式，（$\underline{\hspace{1em}}$）或然式。
3. 重言式與或然式的析取：（$\underline{\hspace{1em}}$）重言式，（$\underline{\hspace{1em}}$）矛盾式，（$\underline{\hspace{1em}}$）或然式。
4. 以重言式爲前後件的蘊涵式：（$\underline{\hspace{1em}}$）重言式，（$\underline{\hspace{1em}}$）矛盾式，（$\underline{\hspace{1em}}$）或然式。
5. 以重言式爲前件、矛盾式爲後件的蘊涵式：（$\underline{\hspace{1em}}$）重言式，（$\underline{\hspace{1em}}$）矛盾式，（$\underline{\hspace{1em}}$）或然式。
6. 以重言式爲前件、或然式爲後件的蘊涵式：（$\underline{\hspace{1em}}$）重言式，（$\underline{\hspace{1em}}$）矛盾式，（$\underline{\hspace{1em}}$）或然式。
7. 以矛盾式爲前、後件的蘊涵式：（$\underline{\hspace{1em}}$）重言式，（$\underline{\hspace{1em}}$）矛盾式，（$\underline{\hspace{1em}}$）或然式。
8. 以矛盾式爲前件、重言式爲後件的蘊涵式：（$\underline{\hspace{1em}}$）重言式，（$\underline{\hspace{1em}}$）矛盾式，（$\underline{\hspace{1em}}$）或然式。
9. 以矛盾式爲前件、或然式爲後件的蘊涵式：（$\underline{\hspace{1em}}$）重言式，（$\underline{\hspace{1em}}$）矛盾式，（$\underline{\hspace{1em}}$）或然式。
10. 以或然式爲前後件的蘊涵式：（$\underline{\hspace{1em}}$）重言式，（$\underline{\hspace{1em}}$）矛盾式，（$\underline{\hspace{1em}}$）或然式。
11. 以或然式爲前件、重言式爲後件的蘊涵式：（$\underline{\hspace{1em}}$）重言式，（$\underline{\hspace{1em}}$）矛盾式，（$\underline{\hspace{1em}}$）或然式。
12. 以或然式爲前件、矛盾式爲後件的蘊涵式：（$\underline{\hspace{1em}}$）重言式，（$\underline{\hspace{1em}}$）矛盾式，（$\underline{\hspace{1em}}$）或然式。
13. 兩端都是重言式的等值式：（$\underline{\hspace{1em}}$）重言式，（$\underline{\hspace{1em}}$）矛盾式，（$\underline{\hspace{1em}}$）或然式。
14. 兩端分別是重言式和矛盾式的等值式：（$\underline{\hspace{1em}}$）重言式，（$\underline{\hspace{1em}}$）矛盾式，（$\underline{\hspace{1em}}$）或然式。
15. 兩端分別是重言式和或然式的等值式：（$\underline{\hspace{1em}}$）重言式，（$\underline{\hspace{1em}}$）矛盾式，（$\underline{\hspace{1em}}$）或然式。
16. 兩端都是矛盾式的等值式：（$\underline{\hspace{1em}}$）重言式，（$\underline{\hspace{1em}}$）矛盾式，（$\underline{\hspace{1em}}$）或然式。
17. 兩端分別是矛盾式和或然式的等值式：（$\underline{\hspace{1em}}$）重言式，（$\underline{\hspace{1em}}$）矛盾式，（$\underline{\hspace{1em}}$）或然式。
18. 兩端都是或然式的等值式：（$\underline{\hspace{1em}}$）重言式，（$\underline{\hspace{1em}}$）矛盾式，（$\underline{\hspace{1em}}$）或然式。

習題 2.7：設 $\varphi$ 和 $\psi$ 爲任意公式。判斷下列命題的眞假

1. $\varphi \land \psi$ 是重言式當且僅當 $\varphi$ 是重言式且 $\psi$ 是重言式。
2. $\varphi \lor \psi$ 是重言式當且僅當或者 $\varphi$ 是重言式或者 $\psi$ 是重言式。
3. $\varphi \rightarrow \psi$ 是重言式當且僅當如果 $\varphi$ 是重言式那麼 $\psi$ 是重言式。
4. $\varphi \leftrightarrow \psi$ 是重言式當且僅當或者 $\varphi$ 和 $\psi$ 都是重言式或者 $\varphi$ 和 $\psi$ 都不是重言式。
5. $\varphi$ 是重言式當且僅當 $\neg \varphi$ 不是重言式。
6. $\varphi \land \psi$ 是矛盾式當且僅當 $\varphi$ 是矛盾式且 $\psi$ 是矛盾式。
7. $\varphi \lor \psi$ 是矛盾式當且僅當或者 $\varphi$ 是矛盾式或者 $\psi$ 是矛盾式。
8. $\varphi \rightarrow \psi$ 是矛盾式當且僅當如果 $\varphi$ 是矛盾式那麼 $\psi$ 是矛盾式。
9. $\varphi \leftrightarrow \psi$ 是矛盾式當且僅當或者 $\varphi$ 和 $\psi$ 都是矛盾式或者 $\varphi$ 和 $\psi$ 都不是矛盾式。
10. $\varphi$ 是矛盾式當且僅當 $\neg \varphi$ 不是矛盾式。
11. $\varphi \land \psi$ 是或然式當且僅當 $\varphi$ 是或然式且 $\psi$ 是或然式。
12. $\varphi \lor \psi$ 是或然式當且僅當或者 $\varphi$ 是或然式或者 $\psi$ 是或然式。
13. $\varphi \rightarrow \psi$ 是或然式當且僅當如果 $\varphi$ 是或然式那麼 $\psi$ 是或然式。
14. $\varphi \leftrightarrow \psi$ 是或然式當且僅當或者 $\varphi$ 和 $\psi$ 都是或然式或者 $\varphi$ 和 $\psi$ 都不是或然式。
15. $\varphi$ 是或然式當且僅當 $\neg \varphi$ 不是或然式。

習題 2.8：設 $\varphi$ 和 $\psi$ 爲任意公式。在每個括號中畫 $\checkmark$ 或 ✗ 表明「對」和「錯」

1. 如果 $\varphi \leftrightarrow \psi$ 是重言式，那麼 $\varphi$ 是重言式當且僅當 $\psi$ 是重言式（$\underline{\hspace{1em}}$），矛盾式（$\underline{\hspace{1em}}$），或然式（$\underline{\hspace{1em}}$）。
2. 如果 $\varphi \leftrightarrow \psi$ 是重言式，那麼 $\varphi$ 是矛盾式當且僅當 $\psi$ 是重言式（$\underline{\hspace{1em}}$），矛盾式（$\underline{\hspace{1em}}$），或然式（$\underline{\hspace{1em}}$）。
3. 如果 $\varphi \leftrightarrow \psi$ 是重言式，那麼 $\varphi$ 是或然式當且僅當 $\psi$ 是重言式（$\underline{\hspace{1em}}$），矛盾式（$\underline{\hspace{1em}}$），或然式（$\underline{\hspace{1em}}$）。
4. 如果 $\varphi \leftrightarrow \psi$ 是矛盾式，那麼 $\varphi$ 是重言式當且僅當 $\psi$ 是重言式（$\underline{\hspace{1em}}$），矛盾式（$\underline{\hspace{1em}}$），或然式（$\underline{\hspace{1em}}$）。
5. 如果 $\varphi \leftrightarrow \psi$ 是矛盾式，那麼 $\varphi$ 是矛盾式當且僅當 $\psi$ 是重言式（$\underline{\hspace{1em}}$），矛盾式（$\underline{\hspace{1em}}$），或然式（$\underline{\hspace{1em}}$）。
6. 如果 $\varphi \leftrightarrow \psi$ 是矛盾式，那麼 $\varphi$ 是或然式當且僅當 $\psi$ 是重言式（$\underline{\hspace{1em}}$），矛盾式（$\underline{\hspace{1em}}$），或然式（$\underline{\hspace{1em}}$）。
7. 如果 $\varphi \leftrightarrow \psi$ 是或然式，那麼。$\varphi$ 是重言式當且僅當 $\psi$ 是重言式（$\underline{\hspace{1em}}$），矛盾式（$\underline{\hspace{1em}}$），或然式（$\underline{\hspace{1em}}$）。
8. 如果 $\varphi \leftrightarrow \psi$ 是或然式，那麼 $\varphi$ 是矛盾式當且僅當 $\psi$ 是重言式（$\underline{\hspace{1em}}$），矛盾式（$\underline{\hspace{1em}}$），或然式（$\underline{\hspace{1em}}$）。
9. 如果 $\varphi \leftrightarrow \psi$ 是或然式，那麼 $\varphi$ 是或然式當且僅當 $\psi$ 是重言式（$\underline{\hspace{1em}}$），矛盾式（$\underline{\hspace{1em}}$），或然式（$\underline{\hspace{1em}}$）。

習題 2.9：設 $\varphi$ 和 $\psi$ 爲任意公式。在每個括號中畫 $\checkmark$ 或 ✗ 表明「對」和「錯」

1. 如果 $\varphi \rightarrow \psi$ 是重言式，那麼 $\varphi$ 是重言式僅當 $\psi$ 是重言式（$\underline{\hspace{1em}}$），矛盾式（$\underline{\hspace{1em}}$），或然式（$\underline{\hspace{1em}}$）。
2. 如果 $\varphi \rightarrow \psi$ 是重言式，那麼 $\varphi$ 是矛盾式僅當 $\psi$ 是重言式（$\underline{\hspace{1em}}$），矛盾式（$\underline{\hspace{1em}}$），或然式（$\underline{\hspace{1em}}$）。
3. 如果 $\varphi \rightarrow \psi$ 是重言式，那麼 $\varphi$ 是或然式僅當 $\psi$ 是重言式（$\underline{\hspace{1em}}$），矛盾式（$\underline{\hspace{1em}}$），或然式（$\underline{\hspace{1em}}$）。
4. 如果 $\varphi \rightarrow \psi$ 是矛盾式，那麼 $\varphi$ 是重言式僅當 $\psi$ 是重言式（$\underline{\hspace{1em}}$），矛盾式（$\underline{\hspace{1em}}$），或然式（$\underline{\hspace{1em}}$）。
5. 如果 $\varphi \rightarrow \psi$ 是矛盾式，那麼 $\varphi$ 是矛盾式僅當 $\psi$ 是重言式（$\underline{\hspace{1em}}$），矛盾式（$\underline{\hspace{1em}}$），或然式（$\underline{\hspace{1em}}$）。
6. 如果 $\varphi \rightarrow \psi$ 是矛盾式，那麼 $\varphi$ 是或然式僅當 $\psi$ 是重言式（$\underline{\hspace{1em}}$），矛盾式（$\underline{\hspace{1em}}$），或然式（$\underline{\hspace{1em}}$）。
7. 如果 $\varphi \rightarrow \psi$ 是或然式，那麼。$\varphi$ 是重言式僅當 $\psi$ 是重言式（$\underline{\hspace{1em}}$），矛盾式（$\underline{\hspace{1em}}$），或然式（$\underline{\hspace{1em}}$）。
8. 如果 $\varphi \rightarrow \psi$ 是或然式，那麼 $\varphi$ 是矛盾式僅當 $\psi$ 是重言式（$\underline{\hspace{1em}}$），矛盾式（$\underline{\hspace{1em}}$），或然式（$\underline{\hspace{1em}}$）。
9. 如果 $\varphi \rightarrow \psi$ 是或然式，那麼 $\varphi$ 是或然式僅當 $\psi$ 是重言式（$\underline{\hspace{1em}}$），矛盾式（$\underline{\hspace{1em}}$），或然式（$\underline{\hspace{1em}}$）。

習題 2.10
說明怎樣用簡化眞值表方法證明一個公式重言蘊涵另一個公式，或重言等值於另一個公式

在以下習題中，對所有公式 $\varphi$ 和 $\psi$，我們以 $\varphi \vDash_0 \psi$ 表示 $\varphi$ 重言蘊涵 $\psi$，以 $\varphi_0,…,\varphi_n$ 表示 $\lbrace \varphi_0,…,\varphi_n\rbrace $ 重言蘊涵 $\psi$。

習題 2.11：設 $\varphi, \psi, \chi$ 爲任意公式。用（簡化）眞值表說明下列命題都成立

1. $ \varphi \vDash_{0} \varphi $
2. $\psi \vDash_{0} \varphi \vee \psi $
3. $\varphi, \psi \vDash_{0} \varphi \wedge \psi $
4. $\varphi \vDash_{0} \varphi \rightarrow \varphi $
5. $\varphi \vDash_{0} \psi \rightarrow \varphi $
6. $\varphi, \varphi \rightarrow \psi \vDash_{0} \psi $
7. $\psi, \neg \psi \vDash_{0} \varphi $
8. $\varphi \vee \psi, \neg \psi \vDash_{0} \varphi $
9. $\neg(\varphi \rightarrow \neg \psi) \vDash_{0} \varphi $
10. $\neg(\varphi \rightarrow \neg \psi) \vDash_{0} \psi $
11. $\varphi \rightarrow \neg \psi, \psi \vDash_{0} \neg \varphi $
12. $\varphi \rightarrow \psi, \chi \rightarrow \varphi \vDash_{0} \chi \rightarrow \psi $
13. $\varphi \wedge \psi \vDash_{0} \psi \wedge \varphi $
14. $\varphi \vee \psi \vDash_{0} \psi \vee \varphi $
15. $\varphi \wedge \psi \vDash_{0} \varphi \vee \psi $
16. $(\varphi \rightarrow \varphi) \rightarrow \psi \vDash_{0} \psi $
17. $\neg \varphi \wedge \neg \psi \vDash_{0} \neg(\varphi \vee \psi) $
18. $\neg \varphi \vee \neg \psi \vDash_{0} \neg(\varphi \wedge \psi) $
19. $\varphi \leftrightarrow \psi, \varphi \vDash_{0} \psi $
20. $\varphi \leftrightarrow \psi, \psi \vDash_{0} \varphi $

習題 2.12：設 $\varphi, \psi$ 爲任意公式。用（簡化）眞值表說明下列每一組中的公式都是重言等值的

1. $\varphi \rightarrow \psi, \neg \varphi \vee \psi, \neg(\varphi \wedge \neg \psi) $
2. $\varphi \vee \psi, \neg(\neg \varphi \wedge \neg \psi), \neg \varphi \rightarrow \psi $
3. $\varphi \wedge \psi, \neg(\neg \varphi \vee \neg \psi), \neg(\varphi \rightarrow \neg \psi) $
4. $\varphi \leftrightarrow \psi,(\varphi \rightarrow \psi) \wedge(\psi \rightarrow \varphi),(\varphi \wedge \psi) \vee(\neg \varphi \wedge \neg \psi)$

習題 2.13：用（簡化）眞值表說明下列各命題都不成立

1. $p \vDash_{0} p \wedge q $
2. $p \vee q \vDash_{0} p $
3. $p \rightarrow q, q \vDash_{0} p $
4. $p \rightarrow q \vDash_{0} q $
5. $p \wedge q \vDash_{0}(p \rightarrow r) \wedge(q \rightarrow r) $
6. $p \vee q \vDash_{0}(p \rightarrow r) \vee(q \rightarrow r) $
7. $p \leftrightarrow q \vDash_{0} p $
8. $p \leftrightarrow q \vDash_{0} q$

習題 2.14：用（簡化）眞值表說明具有下列形式的公式都是重言式

1. $\varphi \leftrightarrow \neg \neg \varphi $
2. $\varphi \rightarrow(\psi \rightarrow \varphi) $
3. $\varphi \rightarrow(\neg \varphi \rightarrow \psi) $
4. $\neg \varphi \rightarrow \neg(\varphi \wedge \psi) $
5. $\neg \psi \rightarrow \neg(\varphi \wedge \psi) $
6. $\neg(\varphi \vee \psi) \leftrightarrow \neg \varphi \wedge \neg \psi $
7. $\neg(\varphi \wedge \psi) \leftrightarrow \neg \varphi \vee \neg \psi $
8. $\neg(\neg \varphi \rightarrow \psi) \rightarrow \neg \varphi $
9. $\neg(\neg \varphi \rightarrow \psi) \rightarrow \neg \psi $
10. $(\varphi \rightarrow \psi) \rightarrow((\varphi \rightarrow \neg \psi) \rightarrow \neg \varphi) $
11. $(\varphi \leftrightarrow \psi) \rightarrow(\psi \leftrightarrow \varphi) $
12. $(\varphi \leftrightarrow(\psi \leftrightarrow \chi)) \leftrightarrow((\varphi \leftrightarrow \psi) \leftrightarrow \chi) $
13. $\varphi \vee\left(\psi_{0} \wedge \cdots \wedge \psi_{k}\right) \leftrightarrow\left(\varphi \vee \psi_{0}\right) \wedge \cdots \wedge\left(\varphi \vee \psi_{k}\right) $
14. $\varphi \wedge\left(\psi_{0} \vee \cdots \vee \psi_{k}\right) \leftrightarrow\left(\varphi \wedge \psi_{0}\right) \vee \cdots \vee\left(\varphi \wedge \psi_{k}\right)$

習題 2.15：用（簡化）眞值表說明具有下列形式的公式都是矛盾式

1. $\varphi \wedge \neg(\neg \varphi \rightarrow \psi) $
2. $(\varphi \rightarrow \neg \varphi) \wedge(\neg \varphi \rightarrow \varphi) $
3. $(\varphi \vee \psi) \wedge(\neg \varphi \wedge \neg \psi) $
4. $\neg(\varphi \rightarrow \psi) \wedge \neg(\psi \rightarrow \varphi) $
5. $(\neg \varphi \rightarrow \neg \psi) \wedge \neg((\neg \varphi \rightarrow \psi) \rightarrow \varphi) $
6. $(\varphi \rightarrow(\psi \rightarrow \chi)) \wedge \neg((\varphi \rightarrow \psi) \rightarrow(\varphi \rightarrow \chi)) $
7. $(\varphi \leftrightarrow \psi) \leftrightarrow(\neg \varphi \leftrightarrow \psi) $
8. $(\varphi \leftrightarrow \psi) \leftrightarrow(\varphi \leftrightarrow \neg \psi)$

習題 2.16：用（簡化）眞值表說明具有下列形式的公式都是或然式

1. $\varphi \rightarrow \psi $
2. $\varphi \rightarrow \neg \neg \neg \varphi $
3. $(\psi \rightarrow \psi) \rightarrow \varphi $
4. $\neg \varphi \rightarrow \neg(\varphi \vee \psi) $
5. $\neg \psi \rightarrow \neg(\varphi \vee \psi) $
6. $(\neg \varphi \rightarrow \psi) \rightarrow((\varphi \rightarrow \psi) \rightarrow \neg \psi) $
7. $(\varphi \leftrightarrow \psi) \rightarrow \varphi \wedge \psi $
8. $(\varphi \leftrightarrow \psi) \rightarrow \neg \varphi \wedge \neg \psi$

習題 2.17：設 $\Gamma = \lbrace \varphi_0,…,\varphi_n\rbrace $ 爲任意的有窮公式集，$\varphi$ 爲任意公式。給出下列命題成立的理由

1. 如果 $\Gamma$ 可滿足，那麼對任何公式集 $\Delta$，$\Gamma \cap \Delta$也可滿足；
2. 如果 $\Gamma$ 不可滿足，那麼對任何有窮公式集 $\Delta$，$\Gamma \cup \Delta$也不可滿足；
3. $\Gamma \cup \lbrace \neg \varphi \rbrace $ 不可滿足當且僅當 $\Gamma$ 重言蘊涵 $\varphi$；
4. 對任意 $i \leqslant n$，$\Gamma$ 不可滿足當且僅當 $\Gamma - \lbrace \psi_i \rbrace $ 重言蘊涵$\neg \psi_i$；
5. 如果 $\Gamma$ 不可滿足，那麼 $\Gamma$ 重言蘊涵 $\varphi$；
6. 如果 $\neg \varphi$ 不可滿足，那麼 $\Gamma$ 重言蘊涵 $\varphi$；
7. 如果 $\Gamma$ 重言蘊涵 $\varphi$，並且 $\Gamma$ 可滿足，那麼 $\varphi$ 也可滿足；
8. 如果 $\Gamma$ 重言蘊涵 $\varphi$ 並且 $\Gamma$ 重言蘊涵 $\neg \varphi$，那麼 $\Gamma$ 不可滿足。

習題 2.18：設 $\varphi, \psi, \varphi_0,…,\varphi_n$ 爲任意公式且 $\Gamma = \lbrace \varphi_0,…,\varphi_n\rbrace $。給出下列命題成立的理由

1. $\varphi$ 重言蘊涵 $\psi$ 當且僅當 $\varphi \rightarrow \psi$ 是重言式；
2. $\varphi$ 重言等值於 $\psi$ 當且僅當 $\varphi \leftrightarrow \psi$ 是重言式，當且僅當 $\psi \rightarrow \varphi$ 與 $\varphi \rightarrow \psi$ 都是重言式；
3. $\Gamma$ 重言蘊涵 $\psi$ 當且僅當 $\varphi_0 \land \cdots \land \varphi_n \rightarrow \psi$ 是重言式；
4. $\varphi_0 \land \cdots \land \varphi_n \rightarrow \psi$ 與 $\varphi_0 \land \cdots \land \varphi_{n-1} \rightarrow (\varphi_n \rightarrow \psi)$ 重言等值；（$n \geqslant 1$）
5. 如果 $\varphi$ 是重言式，那麼 $\Gamma$ 重言蘊涵 $\varphi$；
6. $\Gamma$ 可滿足當且僅當 $\varphi_0 \land \cdots \land \varphi_n$ 或者是或然式或者是重言式；
7. $\Gamma$ 不可滿足當且僅當 $\varphi_0 \land \cdots \land \varphi_n$ 是矛盾式；
8. 如果 $\varphi$ 是重言式，那麼 $\Gamma$ 是可滿足的當且僅當 $\Gamma \cup \lbrace \varphi \rbrace $ 是可滿足的；
9. 如果 $\varphi_i (i \leqslant n)$ 是重言式，那麼 $\Gamma$ 是可滿足的當且僅當 $\Gamma - \lbrace \varphi_i \rbrace $ 是可滿足的；
10. 如果 $\varphi$ 是矛盾式，那麼 $\Gamma \cup \lbrace \varphi \rbrace $ 是不可滿足的；
11. 如果 $\varphi_i (i \leqslant n)$ 是矛盾式，那麼 $\Gamma$ 是不可滿足的。

習題 2.18：將下列公式改寫爲使用波蘭學派記法的公式。完成後，不看下列公式，把那些使用波蘭學派記法的公式再改寫成我們這個語言的公式，然後再和下列公式對照

1. $p \rightarrow q \vee p $
2. $p \rightarrow((p \rightarrow q) \rightarrow q) $
3. $p \wedge \neg(\neg p \rightarrow q) $
4. $(p \rightarrow \neg p) \wedge(\neg p \rightarrow p) $
5. $(p \vee q) \wedge(\neg p \wedge \neg q) $
6. $\neg(p \rightarrow q) \wedge \neg(q \rightarrow p) $
7. $(q \rightarrow q) \rightarrow p $
8. $q \wedge \neg q \rightarrow p $
9. $(p \vee q) \wedge \neg q \rightarrow p $
10. $(q \rightarrow \neg p) \rightarrow(p \rightarrow \neg q) $
11. $(r \rightarrow(p \rightarrow q)) \rightarrow((r \rightarrow p) \rightarrow(r \rightarrow q)) $
12. $\neg p \wedge \neg q \rightarrow \neg(p \vee q) $
13. $\neg p \vee \neg q \rightarrow \neg(p \wedge q) $
14. $(\neg p \rightarrow \neg q) \wedge \neg((\neg p \rightarrow q) \rightarrow p) $
15. $(p \rightarrow(q \rightarrow r)) \wedge \neg((p \wedge q) \rightarrow(p \vee r)) $
16. $(p \leftrightarrow q) \rightarrow(\neg p \vee \neg q) $
17. $(\neg p \vee q) \rightarrow(p \wedge q \rightarrow \neg q) $
18. $(p \leftrightarrow q) \rightarrow \neg q \wedge \neg p$

The article was recently updated on Saturday, September 2, 2023, 13:39:40 by 王小花.