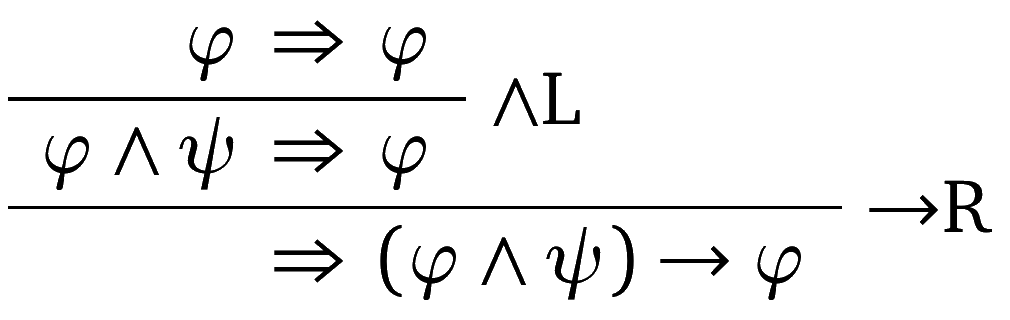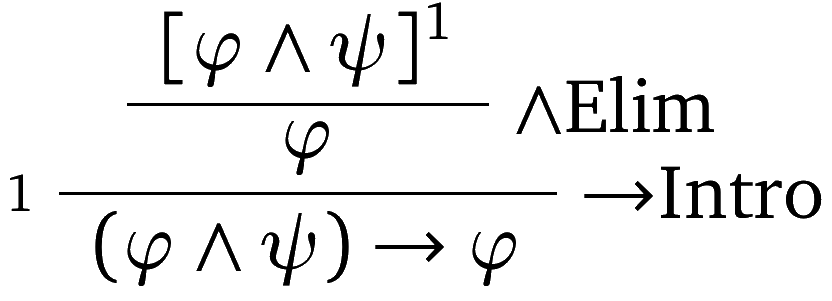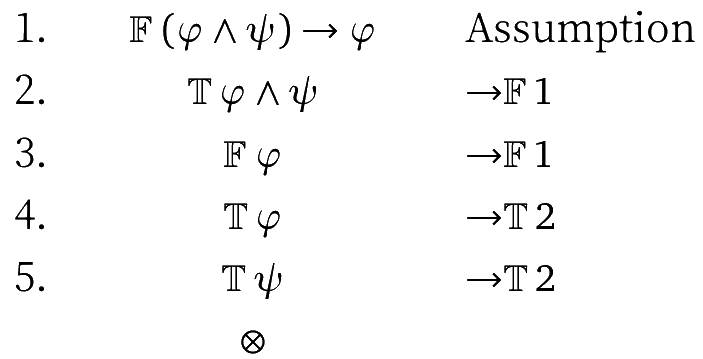This chapter collects general material on derivation systems. A text-book using a specific system can insert the introduction section plus the relevant survey section at the beginning of the chapter introducing that system.

Introduction

Logics commonly have both a semantics and a derivation system. The semantics concerns concepts such as truth, satisfiability, validity, and entailment. The purpose of derivation systems is to provide a purely syntactic method of establishing entailment and validity. They are purely syntactic in the sense that a derivation in such a system is a finite syntactic object, usually a sequence (or other finite arrangement) of sentences or formulas. Good derivation systems have the property that any given sequence or arrangement of sentences or formulas can be verified mechanically to be “correct.''

The simplest (and historically first) derivation systems for first-order logic were axiomatic. A sequence of formulas counts as a derivation in such a system if each individual formula in it is either among a fixed set of “axioms’’ or follows from formulas coming before it in the sequence by one of a fixed number of “inference rules’’—and it can be mechanically verified if a formula is an axiom and whether it follows correctly from other formulas by one of the inference rules. Axiomatic proof systems are easy to describe—and also easy to handle meta-theoretically—but derivations in them are hard to read and understand, and are also hard to produce.

Other derivation systems have been developed with the aim of making it easier to construct derivations or easier to understand derivations once they are complete. Examples are natural deduction, truth trees, also known as tableaux proofs, and the sequent calculus. Some derivation systems are designed especially with mechanization in mind, e.g., the resolution method is easy to implement in software (but its derivations are essentially impossible to understand). Most of these other proof systems represent derivations as trees of formulas rather than sequences. This makes it easier to see which parts of a derivation depend on which other parts.

So for a given logic, such as first-order logic, the different derivation systems will give different explications of what it is for a sentence to be a theorem and what it means for a sentence to be derivable from some others. However that is done (via axiomatic derivations, natural deductions, sequent derivations, truth trees, resolution refutations), we want these relations to match the semantic notions of validity and entailment. Let’s write $\vdash \varphi$ for “$\varphi$ is a theorem’’ and “$\Gamma \vdash \varphi$’’ for “$\varphi$ is derivable from $\Gamma$.’’ However $\vdash$ is defined, we want it to match up with $\vDash$, that is:

1. $\vdash \varphi$ if and only if $\vDash \varphi$
2. $\Gamma \vdash \varphi$ if and only if $\Gamma \vDash \varphi$

The “only if’’ direction of the above is called soundness. A derivation system is sound if derivability guarantees entailment (or validity). Every decent derivation system has to be sound; unsound derivation systems are not useful at all. After all, the entire purpose of a derivation is to provide a syntactic guarantee of validity or entailment. We’ll prove soundness for the derivation systems we present.

The converse “if’’ direction is also important: it is called completeness. A complete derivation system is strong enough to show that $\varphi$ is a theorem whenever $\varphi$ is valid, and that $\Gamma \vdash \varphi$ whenever $\Gamma \vDash \varphi$. Completeness is harder to establish, and some logics have no complete derivation systems. First-order logic does. Kurt G"odel was the first one to prove completeness for a derivation system of first-order logic in his 1929 dissertation.

Another concept that is connected to derivation systems is that of consistency. A set of sentences is called inconsistent if anything whatsoever can be derived from it, and consistent otherwise. Inconsistency is the syntactic counterpart to unsatisfiablity: like unsatisfiable sets, inconsistent sets of sentences do not make good theories, they are defective in a fundamental way. Consistent sets of sentences may not be true or useful, but at least they pass that minimal threshold of logical usefulness. For different derivation systems the specific definition of consistency of sets of sentences might differ, but like $\vdash$, we want consistency to coincide with its semantic counterpart, satisfiability. We want it to always be the case that $\Gamma$ is consistent if and only if it is satisfiable. Here, the “if’’ direction amounts to completeness (consistency guarantees satisfiability), and the “only if’’ direction amounts to soundness (satisfiability guarantees consistency). In fact, for classical first-order logic, the two versions of soundness and completeness are equivalent.

The Sequent Calculus

While many derivation systems operate with arrangements of sentences, the sequent calculus operates with sequents. A sequent is an expression of the form

$$\varphi_1, \cdots, \varphi_m \Rightarrow \psi_1, \cdots, \psi_m,$$

that is a pair of sequences of sentences, separated by the sequent symbol $\Rightarrow$. Either sequence may be empty. a derivation in the sequent calculus is a tree of sequents, where the topmost sequents are of a special form (they are called “initial sequents’’ or “axioms’’) and every other sequent follows from the sequents immediately above it by one of the rules of inference. The rules of inference either manipulate the sentences in the sequents (adding, removing, or rearranging them on either the left or the right), or they introduce a complex formula in the conclusion of the rule. For instance, the $\color{red}\land\text{L}$ rule allows the inference from $\varphi, \Gamma \Rightarrow \Delta$ to $\varphi \land \psi, \Gamma \Rightarrow \Delta$, and the $\color{red}\rightarrow\text{R}$ allows the inference from $\varphi, \Gamma \Rightarrow \Delta, \psi$ to $\Gamma \Rightarrow \Delta, \varphi \rightarrow \psi$, for any $\Gamma$, $\Delta$, $\varphi$, and $\psi$. (In particular, $\Gamma$ and $\Delta$ may be empty.)

The $\vdash$ relation based on the sequent calculus is defined as follows: $\Gamma \vdash \varphi$ iff there is some sequence $\Gamma_0$ such that every $\varphi$ in $\Gamma_0$ is in $\Gamma$ and there is a derivation with the sequent $\Gamma_0 \Rightarrow \varphi$ at its root. $\varphi$ is a theorem in the sequent calculus if the sequent $\Rightarrow \varphi$ has a derivation. For instance, here is a derivation that shows that $\vdash (\varphi \land \psi) \rightarrow \varphi$:

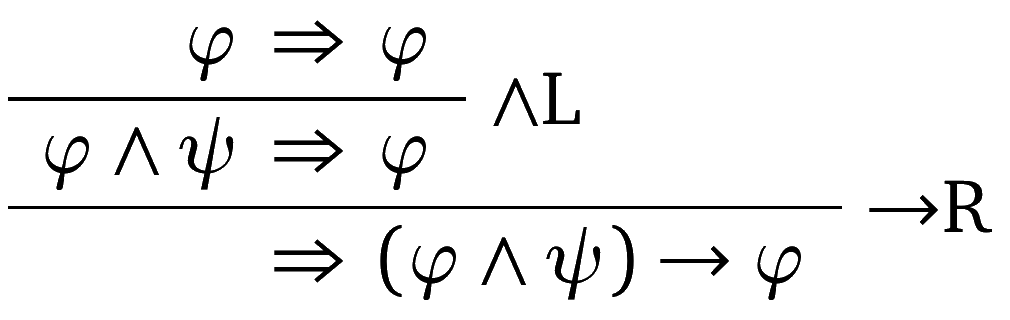
A set $\Gamma$ is inconsistent in the sequent calculus if there is a derivation of $\Gamma_0 \Rightarrow$ (where every $\varphi \in \Gamma_0$ is in $\Gamma$ and the right side of the sequent is empty). Using the rule WR, any sentence can be derived from an inconsistent set.

The sequent calculus was invented in the 1930s by Gerhard Gentzen. Because of its systematic and symmetric design, it is a very useful formalism for developing a theory of derivations. It is relatively easy to find derivations in the sequent calculus, but these derivations are often hard to read and their connection to proofs are sometimes not easy to see. It has proved to be a very elegant approach to derivation systems, however, and many logics have sequent calculus systems.

Natural Deduction

Natural deduction is a derivation system intended to mirror actual reasoning (especially the kind of regimented reasoning employed by mathematicians). Actual reasoning proceeds by a number of “natural’’ patterns. For instance, proof by cases allows us to establish a conclusion on the basis of a disjunctive premise, by establishing that the conclusion follows from either of the disjuncts. Indirect proof allows us to establish a conclusion by showing that its negation leads to a contradiction. Conditional proof establishes a conditional claim “if \cdots then \cdots’’ by showing that the consequent follows from the antecedent. Natural deduction is a formalization of some of these natural inferences. Each of the logical connectives and quantifiers comes with two rules, an introduction and an elimination rule, and they each correspond to one such natural inference pattern. For instance, $\color{red}\rightarrow\text{Intro}$ corresponds to conditional proof, and $\color{red}\lor\text{Elim}$ to proof by cases. A particularly simple rule is $\color{red}\land\text{Elim}$ which allows the inference from $\varphi \land \psi$ to $\varphi$ (or $\psi$).

One feature that distinguishes natural deduction from other derivation systems is its use of assumptions. a derivation in natural deduction is a tree of formulas. A single formula stands at the root of the tree of formulas, and the “leaves’’ of the tree are formulas from which the conclusion is derived. In natural deduction, some leaf formulas play a role inside the derivation but are “used up’’ by the time the derivation reaches the conclusion. This corresponds to the practice, in actual reasoning, of introducing hypotheses which only remain in effect for a short while. For instance, in a proof by cases, we assume the truth of each of the disjuncts; in conditional proof, we assume the truth of the antecedent; in indirect proof, we assume the truth of the negation of the conclusion. This way of introducing hypothetical assumptions and then doing away with them in the service of establishing an intermediate step is a hallmark of natural deduction. The formulas at the leaves of a natural deduction derivation are called assumptions, and some of the rules of inference may “discharge’’ them. For instance, if we have a derivation of $\psi$ from some assumptions which include $\varphi$, then the $\color{red}\rightarrow\text{Intro}$ rule allows us to infer $\varphi \rightarrow \psi$ and discharge any assumption of the form $\varphi$. (To keep track of which assumptions are discharged at which inferences, we label the inference and the assumptions it discharges with a number.) The assumptions that remain undischarged at the end of the derivation are together sufficient for the truth of the conclusion, and so a derivation establishes that its undischarged assumptions entail its conclusion.

The relation $\Gamma \vdash \varphi$ based on natural deduction holds iff there is a derivation in which $\varphi$ is the last sentence in the tree, and every leaf which is undischarged is in $\Gamma$. $\varphi$ is a theorem in natural deduction iff there is a derivation in which $\varphi$ is the last sentence and all assumptions are discharged. For instance, here is a derivation that shows that $\vdash (\varphi \land \psi) \rightarrow \varphi$:

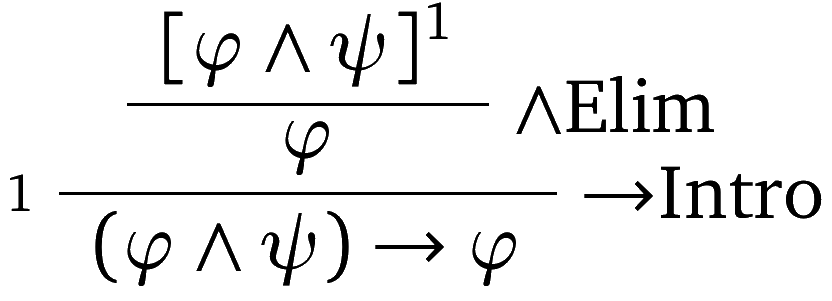
The label $1$ indicates that the assumption $\varphi \land \psi$ is discharged at the $\color{red}\rightarrow\text{Intro}$ inference.

A set $\Gamma$ is inconsistent iff $\Gamma \vdash \bot$ in natural deduction. The rule $\bot_{I}$ makes it so that from an inconsistent set, any sentence can be derived.

Natural deduction systems were developed by Gerhard Gentzen and Stanislaw Jaskowski in the 1930s, and later developed by Dag Prawitz and Frederic Fitch. Because its inferences mirror natural methods of proof, it is favored by philosophers. The versions developed by Fitch are often used in introductory logic textbooks. In the philosophy of logic, the rules of natural deduction have sometimes been taken to give the meanings of the logical operators (“proof-theoretic semantics’’).

Tableaux

While many derivation systems operate with arrangements of sentences, tableaus operate with signed formulas. a signed formula is a pair consisting of a truth value sign ($\mathbb{T}$ or $\mathbb{F}$) and a sentence

$$\mathbb{T} \varphi \text{ or } \mathbb{F} \varphi.$$

a tableau consists of signed formulas arranged in a downward-branching tree. It begins with a number of assumptions and continues with signed formulas which result from one of the signed formulas above it by applying one of the rules of inference. Each rule allows us to add one or more signed formulas to the end of a branch, or two signed formulas side by side—in this case a branch splits into two, with the two added signed formulas forming the ends of the two branches.

A rule applied to a complex signed formula results in the addition of signed formulas which are immediate sub-formulas. They come in pairs, one rule for each of the two signs. For instance, the $\land\mathbb{T}$ rule applies to ${\mathbb{T}}{\varphi \land \psi}$, and allows the addition of both the two signed formulas ${\mathbb{T}}{\varphi}$ and ${\mathbb{T}}{\psi}$ to the end of any branch containing ${\mathbb{T}}{\varphi \land \psi}$, and the rule ${\varphi \land \psi \mathbb{F}}$ allows a branch to be split by adding ${\mathbb{F}}{\varphi}$ and ${\mathbb{F}}{\psi}$ side-by-side. a tableau is closed if every one of its branches contains a matching pair of signed formulas ${\mathbb{T}}{\varphi}$ and ${\mathbb{F}}{\varphi}$.

The $\vdash$ relation based on tableaus is defined as follows: $\Gamma \vdash \varphi$ iff there is some finite set $\Gamma_0 = \lbrace \psi_1, \cdots, \psi_n\rbrace \subseteq \Gamma$ such that there is a closed tableau for the assumptions

$$\lbrace {\mathbb{F}}{\varphi}, {\mathbb{T}}{\psi_1}, \cdots, {\mathbb{T}}{\psi_n}\rbrace $$

For instance, here is a closed tableau that shows that $\vdash (\varphi \land \psi) \rightarrow \varphi$:

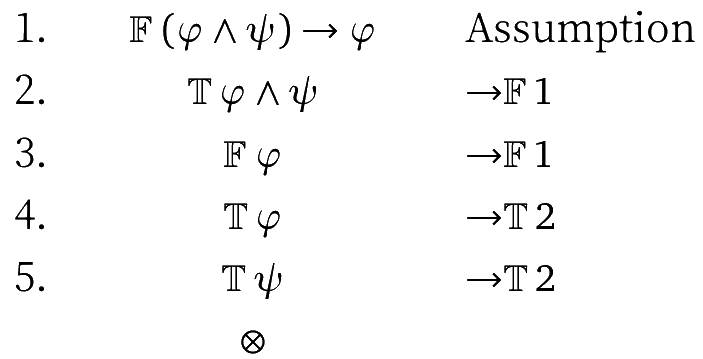
A set $\Gamma$ is inconsistent in the tableau calculus if there is a closed tableau for assumptions

$$\lbrace {\mathbb{T}}{\psi_1}, \cdots, {\mathbb{T}}{\psi_n}\rbrace$$

for some $\psi_i \in \Gamma$.

tableaus were invented in the 1950s independently by Evert Beth and Jaakko Hintikka, and simplified and popularized by Raymond Smullyan. They are very easy to use, since constructing a tableau is a very systematic procedure. Because of the systematic nature of tableaus, they also lend themselves to implementation by computer. However, a tableau is often hard to read and their connection to proofs are sometimes not easy to see. The approach is also quite general, and many different logics have tableau systems. tableaus also help us to find structures that satisfy given (sets of) sentences: if the set is satisfiable, it won’t have a closed tableau, i.e., any tableau will have an open branch. The satisfying structure can be “read off’’ an open branch, provided every rule it is possible to apply has been applied on that branch. There is also a very close connection to the sequent calculus: essentially, a closed tableau is a condensed derivation in the sequent calculus, written upside-down.

Axiomatic Derivation

Axiomatic derivations are the oldest and simplest logical derivation systems. Its derivations are simply sequences of sentences. A sequence of sentences conunts as a correct derivation if every sentence $\varphi$ in it satisfies one of the following conditions: > 1. $\varphi$ is an axiom, or> 1. $\varphi$ is an element of a given set $\Gamma$ of sentences, or> 1. $\varphi$ is justified by a rule of inference. To be an axiom, $\varphi$ has to have the form of on of a number of fixed sentence schemas. There are many sets of axiom schemas that provide a satisfactory (sound and complete) derivation system for first-order logic. Some are organized according to the connectives they govern, e.g., the schemas

$$\varphi \rightarrow (\psi \rightarrow \varphi) \quad\quad \psi \rightarrow (\psi \lor \chi) \quad\quad (\psi \land \chi) \rightarrow \psi$$

are common axioms that govern $\rightarrow$, $\lor$ and $\land$. Some axiom systems aim at a minimal number of axioms. Depending on the connectives that are taken as primitives, it is even possible to find axiom systems that consist of a single axiom.

A rule of inference is a conditional statement that gives a sufficient condition for a sentence in a derivation to be justified. Modus ponens is one very common such rule: it says that if $\varphi$ and $\varphi \rightarrow \psi$ are already justified, then $\psi$ is justified. This means that a line in a derivation containing the sentence $\psi$ is justified, provided that both $\varphi$ and $\varphi \rightarrow \psi$ (for some sentence $\varphi$) appear in the derivation before $\psi$.

The $\vdash$ relation based on axiomatic derivations is defined as follows: $\Gamma \vdash \varphi$ iff there is a derivation with the sentence $\varphi$ as its last formula (and $\Gamma$ is taken as the set of sentences in that derivation which are justified by (2) above). $\varphi$ is a theorem if $\varphi$ has a derivation where $\Gamma$ is empty, i.e., every sentence in the derivation is justfied either by (1) or (3). For instance, here is a derivation that shows that $\vdash \varphi \rightarrow (\psi \rightarrow (\psi \lor \varphi))$:

1. $\psi \rightarrow (\psi \lor \varphi)$
2. $(\psi \rightarrow (\psi \lor \varphi)) \rightarrow (\varphi \rightarrow (\psi \rightarrow (\psi \lor \varphi)))$
3. $\varphi \rightarrow (\psi \rightarrow (\psi \lor \varphi))$

The sentence on line 1 is of the form of the axiom $\varphi \rightarrow (\varphi \lor \psi)$ (with the roles of $\varphi$ and $\psi$ reversed). The sentence on line 2 is of the form of the axiom $\varphi \rightarrow (\psi \rightarrow \varphi)$. Thus, both lines are justified. Line 3 is justified by modus ponens: if we abbreviate it as $\theta$, then line 2 has the form $\chi \rightarrow \theta$, where $\chi$ is $\psi \rightarrow (\psi \lor \varphi)$, i.e., line 1.

A set $\Gamma$ is inconsistent if $\Gamma \vdash \bot$. A complete axiom system will also prove that $\bot \rightarrow \varphi$ for any $\varphi$, and so if $\Gamma$ is inconsistent, then $\Gamma \vdash \varphi$ for any $\varphi$.

Systems of axiomatic derivations for logic were first given by Gottlob Frege in his 1879 \W{Begriffsschrift}, which for this reason is often considered the first work of modern logic. They were perfected in Alfred North Whitehead and Bertrand Russell’s \W{Principia Mathematica} and by David Hilbert and his students in the 1920s. They are thus often called “Frege systems’’ or “Hilbert systems.’’ They are very versatile in that it is often easy to find an axiomatic system for a logic. Because derivations have a very simple structure and only one or two inference rules, it is also relatively easy to prove things about them. However, they are very hard to use in practice, i.e., it is difficult to find and write proofs.

The article was recently updated on Friday, October 7, 2022, 02:21:05 by 王小花.